
(本小题满分12分)设函数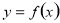 定义在R上,对于任意实数
定义在R上,对于任意实数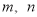 ,恒有
,恒有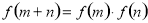 ,且当
,且当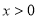 时,
时,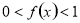
(1)求证: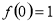 且当
且当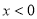 时,
时,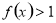
(2)求证: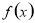 在R上是减函数;
在R上是减函数;
(3)设集合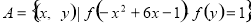 ,
,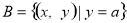 ,且
,且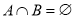 ,求实数
,求实数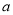 的取值范围。
的取值范围。
(1)(2)证明略,(3)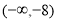
【解析】
试题分析:首先用赋值法求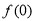 ,然后利用当
,然后利用当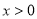 时,
时, ,由于
,由于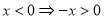 ,则
,则 ,再赋值
,再赋值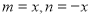 ,找出
,找出 与
与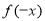 的关系为
的关系为 即可.第二步先取
即可.第二步先取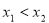 ,把
,把 写
写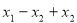 ,有
,有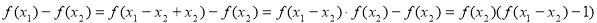 ,因为
,因为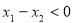 ,
,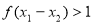 ,
,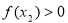 ,进而判断
,进而判断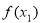 和
和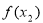 的大小.第三步
的大小.第三步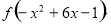
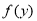
 ,则
,则 ,有
,有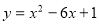 ,两个点集
,两个点集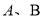 交集为空,即两线无交点,则直线
交集为空,即两线无交点,则直线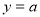 在抛物线定点下方,即
在抛物线定点下方,即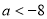 即可.
即可.
试题解析:(1)证明:∵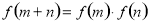 ,
,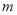 、
、 为任意实数,取
为任意实数,取 ,则有
,则有
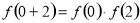 ,∵当
,∵当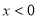 时,
时, ,∴
,∴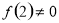 ,∴
,∴ 当
当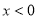 时,
时,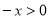 ,∴
,∴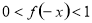 ,则
,则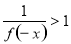 取
取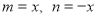 ,则
,则 则
则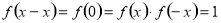 ,∴
,∴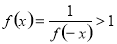
(2)证明:由(1)及题设可知,在R上 在R上
在R上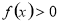
∴
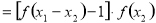
∵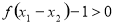
 ,∴
,∴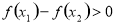
即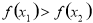 所以
所以 在R上是减函数
在R上是减函数
(3)【解析】
在集合A中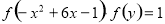 由已知条件,有
由已知条件,有
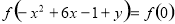 ,∴
,∴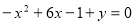 ,即
,即 在集合B中,有
在集合B中,有
∵ ,则抛物线
,则抛物线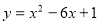 与直线
与直线 无交点
无交点
∵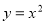
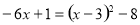 ,∴
,∴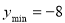 ,∴
,∴
即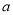 的取值范围是(
的取值范围是(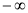 ,-8)。
,-8)。
考点:1.赋值法;2.利用抽象函数关系;3.解不等式;4.两曲线交点问题;


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014-2015学年云南德宏州芒市高一上学期期末考试数学试卷(解析版) 题型:选择题
函数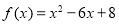 在
在 上的最大值和最小值分别为 ( )
上的最大值和最小值分别为 ( )
A. 15, 3 B. 15, 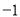 C. 8 ,
C. 8 , 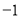 D.20,
D.20, 
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省潍坊市高一上学期10月月考数学试卷(解析版) 题型:填空题
函数f(x)在R上为奇函数,且当x>0时,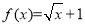 ,则x<0时的解析式为f(x)=________.
,则x<0时的解析式为f(x)=________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省高一上学期期中考试数学试卷(解析版) 题型:解答题
(本小题满分10分)已知在半径为10的圆O中,弦AB的长为10。
(1)求弦AB所对的圆心角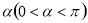 的大小。
的大小。
(2)求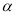 所在的扇形弧长
所在的扇形弧长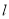 及弧所在的弓形的面积S。
及弧所在的弓形的面积S。
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省高一上学期期中考试数学试卷(解析版) 题型:选择题
函数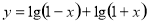 的图像关于( )
的图像关于( )
A. 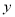 轴对称 B.
轴对称 B.  轴对称
轴对称
C. 原点对称 D. 点(1,1)对称
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省赣州市北校高二1月月考文科数学试卷(解析版) 题型:填空题
已知P是双曲线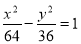 上一点,F1,F2是双曲线的两个焦点,若|PF1|=17,则|PF2|的值为________.
上一点,F1,F2是双曲线的两个焦点,若|PF1|=17,则|PF2|的值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com