已知f(x)=log3(3+x)+log3(3-x).
(1)求f(x)的定义域和值域;
(2)判断函数f(x)的奇偶性,并说明理由;
(3)写出函数f(x)的递增区间和递减区间.
解:(1))根据题意可得
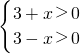
,解不等式可得-3<x<3
∴定义域为(-3,3)
f(x)=log
3(3+x)+log
3(3-x)=log
3(-x
2+9)
令t═-x
2+9,则t∈(0,9],f(x)∈(-∞,2]
∴值域为(-∞,2].
(2)∵定义域为(-3,3)关于原点对称
∵f(-x)=log
3(3-x)+log
3(3+x)=f(x),
所以函数f(x)为偶函数.
(3)∵t=9-x
2在(-3,0]上单调递增.在(0,3]上单调递减
∵函数y=log
3t在(0,+∞)单调递增
根据复合函数的单调性可得函数f(x)的单调增区间(-3,0],单调减区间[0,3)
分析:(1)根据题意可得
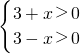
解不等式可得函数的定义域
f(x)=log
3(3+x)(3-x),令t=(3+x)(3-x)=-x
2+9∈(0,9],从而可得函数的值域
(2)结合(1)的定义域,计算可得f(-x)=log
3(3-x)+log
3(3+x)=f(x),从而可得函数为偶函数
(3)t=-x
2+9在(-3,0]上单调递增,[0,3)上单调递减,函数y=log
3t在(0,+∞)单调递增
根据复合函数的单调性可得函数f(x)的单调增区间(-3,0],单调减区间[0,3)
点评:本题主要考查了对数函数的定义域的求解,复合函数的值域的求解,函数奇偶性的判断,复合函数的单调性的判断,综合运用了函数的性质.

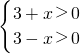 ,解不等式可得-3<x<3
,解不等式可得-3<x<3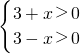 解不等式可得函数的定义域
解不等式可得函数的定义域

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案