
| A. | (-∞,-2] | B. | (-∞,-$\frac{25}{12}$] | C. | (-∞,50] | D. | (-∞,-1] |
分析 根据题意可得,x=-3和x=-2是方程ax2+(b-8)x-a-ab=0的两个根,求出a=-3,b=5;-3x2+5x+c≤0在[1,4]上恒成立即:c≤3x2-5x在[1,4]上恒成立;
解答 解:根据题意可得,x=-3和x=-2是方程ax2+(b-8)x-a-ab=0的两个根,且a<0;
利用韦达定理可得-3+2=-$\frac{8-b}{a}$,-3×2=$\frac{-a-ab}{a}$,
求得:a=-3,b=5;
故函数f(x)=-3$(x+\frac{1}{2})^{2}$+$\frac{75}{4}$,
不等式ax2+bx+c≤0即:-3x2+5x+c≤0,
-3x2+5x+c≤0在[1,4]上恒成立即:c≤3x2-5x在[1,4]上恒成立;
令h(x)=3x2-5x,x∈[1,4],h(x)的最小值为:h(1)=-2;
故c≤-2.
故选:A.
点评 本题主要考查了二次函数根与韦达定理、分类参数法求函数最值等知识点,属基础题.


科目:高中数学 来源: 题型:选择题
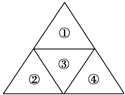 如图,要给①,②,③,④四块区域分别涂上五种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同颜色,则不同的涂色方法种数为( )
如图,要给①,②,③,④四块区域分别涂上五种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同颜色,则不同的涂色方法种数为( )| A. | 320 | B. | 160 | C. | 96 | D. | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{\sqrt{14}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
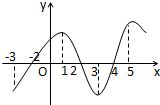
| A. | 在区间(-3,1)内y=f(x)是增函数 | B. | 在区间(1,3)内y=f(x)是减函数 | ||
| C. | 在区间(4,5)内y=f(x)是增函数 | D. | 在x=2时,y=f(x)取得极小值 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com