
���� ���Ȼ������������������������ʽ���������ȷ��$\overrightarrow{OP}$��$\overrightarrow{OA}$������ͶӰΪ$\frac{\overrightarrow{OA}•\overrightarrow{OP}}{|\overrightarrow{OA}|}=\frac{3x+\sqrt{3}y}{2\sqrt{3}}=\frac{\sqrt{3}}{2}x+\frac{1}{2}y$�������伸����������ֵ��
��� �⣺����֪�õ�ƽ��������ͼ��P��������Ϊ��Ӱ���֣�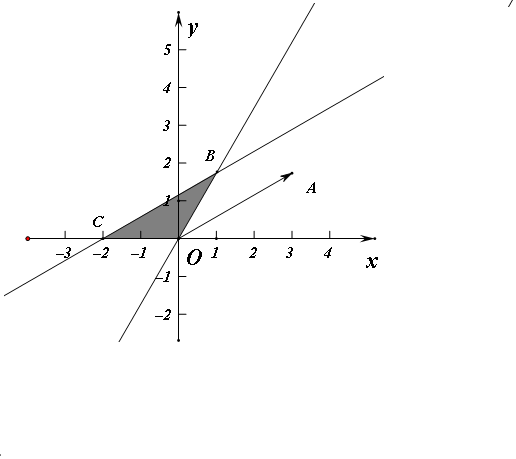 ��$\left\{\begin{array}{l}{\sqrt{3}x-y=0}\\{x-\sqrt{3}y+2=0}\end{array}\right.$�õ�C��-2��0��B��1��$\sqrt{3}$�������������Ϊ$\frac{1}{2}��2��\sqrt{3}=\sqrt{3}$��
��$\left\{\begin{array}{l}{\sqrt{3}x-y=0}\\{x-\sqrt{3}y+2=0}\end{array}\right.$�õ�C��-2��0��B��1��$\sqrt{3}$�������������Ϊ$\frac{1}{2}��2��\sqrt{3}=\sqrt{3}$��
��$\overrightarrow{OP}$��$\overrightarrow{OA}$������ͶӰΪ$\frac{\overrightarrow{OA}•\overrightarrow{OP}}{|\overrightarrow{OA}|}=\frac{3x+\sqrt{3}y}{2\sqrt{3}}=\frac{\sqrt{3}}{2}x+\frac{1}{2}y$������y=$-\sqrt{3}x+2z$����Bʱz���
���ԣ�$\overrightarrow{OP}$��$\overrightarrow{OA}$������ͶӰ�����ֵΪ$-\sqrt{3}+2\sqrt{3}=\sqrt{3}$��
�ʴ�Ϊ��$\sqrt{3}$��$\sqrt{3}$��
���� ���⿼���˼����Թ滮���⣻��ȷ��������������Ŀ�꺯���ļ������������ֵ�ǹؼ���


 ���ѵ����Ԫ��ĩ���100��ϵ�д�
���ѵ����Ԫ��ĩ���100��ϵ�д� ��˼άС�ھ�100����ҵ��ϵ�д�
��˼άС�ھ�100����ҵ��ϵ�д� ��ʦָ��һ��ͨϵ�д�
��ʦָ��һ��ͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\frac{��}{3}$��$\frac{22��}{3}$ | B�� | $-\frac{7��}{9}$��$\frac{11��}{9}$ | C�� | $\frac{20��}{3}$��$\frac{22��}{9}$ | D�� | $\frac{��}{2}$��$-\frac{��}{2}+2k��k��Z$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�-2] | B�� | ��-�ޣ�-$\frac{25}{12}$] | C�� | ��-�ޣ�50] | D�� | ��-�ޣ�-1] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����f��x������С������Ϊ2�� | |
| B�� | f��x����ͼ�����ֱ��$x=\frac{��}{8}$ | |
| C�� | �Գ�f��x�������ֵΪ$\sqrt{2}$ | |
| D�� | ��f��x����ͼ������ƽ��$\frac{��}{8}$��������ƽ��$\frac{1}{2}$����λ���Ⱥ��õ�һ���溯����ͼ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com