解:(1)求导函数,可得
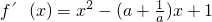
∵a>0,∴
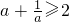
∴
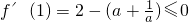
,当且仅当a=1时,等号成立
即当a=1时,f(x)在点(1,f(1))处切线斜率最大,该切线方程为y=

;
(2)当a=2时,f(x)=

x
3-

x
2+x
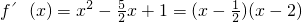
令f′(x)>0,可得
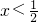
或x>2,此时函数单调递增;
令f′(x)<0,可得
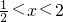
,此时函数单调递减;
要使函数f(x)在区间(k-

,k+

)内不是单调函数,则

或
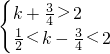
∴
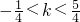
或
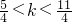
(3)f(x)的图象不经过第四象限,即f(x)≥0在x∈[0,+∞)恒成立.
令f′(x)=0得x
1=a,x
2=

.
①当a<0时,f(x)在[0,+∞)单调递增,符合题意;
②当a>0时,∵x∈[0,+∞),
∴f(x)
min=min{f(0),f(a),f(

)},
∵f(0)=0,∴
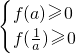
得

≤a≤

,
综上所得,a的取值范围是a<0或

≤a≤

.(13分)
分析:(1)求导函数,可得
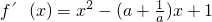
,利用基本不等式,可知a=1时,f(x)在点(1,f(1))处切线斜率最大,从而可求切线方程;
(2)当a=2时,f(x)=

x
3-

x
2+x,求导函数
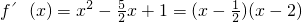
,从而可知
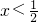
或x>2时,函数单调递增,
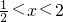
时函数单调递减,要使函数f(x)在区间(k-

,k+

)内不是单调函数,则

或
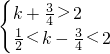
,从而可求实数k的取值范围;
(3)f(x)的图象不经过第四象限,即f(x)≥0在x∈[0,+∞)恒成立.分类讨论:①当a<0时,f(x)在[0,+∞)单调递增,符合题意;②当a>0时,f(x)
min=min{f(0),f(a),f(

)}≥0即可,从而可求a的取值范围.
点评:本题重点考查导数知识的运用,考查导数的几何意义,考查函数的单调性,考查函数的最值,同时考查学生分析解决问题的能力,综合性强.

 x3-
x3- (a+
(a+ )x2+x(a∈R,a≠0).
)x2+x(a∈R,a≠0). ,k+
,k+ )内不是单调函数,求实数k的取值范围;
)内不是单调函数,求实数k的取值范围;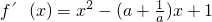
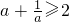
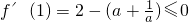 ,当且仅当a=1时,等号成立
,当且仅当a=1时,等号成立 ;
; x3-
x3- x2+x
x2+x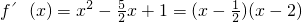
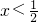 或x>2,此时函数单调递增;
或x>2,此时函数单调递增;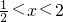 ,此时函数单调递减;
,此时函数单调递减; ,k+
,k+ )内不是单调函数,则
)内不是单调函数,则 或
或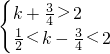
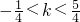 或
或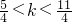
 .
. )},
)},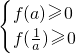
 ≤a≤
≤a≤ ,
, ≤a≤
≤a≤ .(13分)
.(13分)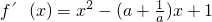 ,利用基本不等式,可知a=1时,f(x)在点(1,f(1))处切线斜率最大,从而可求切线方程;
,利用基本不等式,可知a=1时,f(x)在点(1,f(1))处切线斜率最大,从而可求切线方程; x3-
x3- x2+x,求导函数
x2+x,求导函数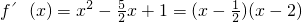 ,从而可知
,从而可知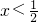 或x>2时,函数单调递增,
或x>2时,函数单调递增,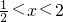 时函数单调递减,要使函数f(x)在区间(k-
时函数单调递减,要使函数f(x)在区间(k- ,k+
,k+ )内不是单调函数,则
)内不是单调函数,则 或
或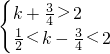 ,从而可求实数k的取值范围;
,从而可求实数k的取值范围; )}≥0即可,从而可求a的取值范围.
)}≥0即可,从而可求a的取值范围.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<