
【题目】如图,在直三棱柱ABC﹣A1B1C1中,平面A1BC⊥侧面A1B1BA,且AA1=AB=BC=2,则AC与平面A1BC所成角为( ) 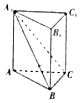
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:如图,AB1∩A1B=D,连结CD, ∵AA1=AB,∴AD⊥A1B,
∵平面A1BC⊥侧面A1ABB1 , 且平面A1BC∩侧面A1ABB1=A1B,
∴AD⊥平面A1BC,
则CD是AC在平面A1BC内的射影,
∴∠ACD即为直线AC与平面A1BC所成的角,
又BC平面A1BC,
所以AD⊥BC,
因为三棱柱ABC﹣﹣﹣A1B1C1是直三棱柱,
则AA1⊥底面ABC,
所以AA1⊥BC.
又AA1∩AD=A,从而BC⊥侧面A1ABB1 ,
又AB侧面A1ABB1 , 故AB⊥BC
∵AA1=AB=BC=2,∴AC= ![]() ,AD=
,AD= ![]()
∴sin∠ACD= ![]() ,∴∠ACD=
,∴∠ACD= ![]() ,
,
故选A.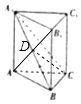
【考点精析】通过灵活运用空间角的异面直线所成的角,掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则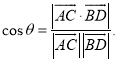 即可以解答此题.
即可以解答此题.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】某省每年损失耕地20万亩,每亩耕地价值24000元,为了减少耕地损失,决定按耕地价格的t%征收耕地占用税,这样每年的耕地损失可减少 ![]() t万亩,为了既可减少耕地的损失又保证此项税收一年不少于9000万元,则t的取值范围是( )
t万亩,为了既可减少耕地的损失又保证此项税收一年不少于9000万元,则t的取值范围是( )
A.[1,3]
B.[3,5]
C.[5,7]
D.[7,9]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an},{bn}中,已知a1=2,b1=4,且﹣an , bn , an+1成等差数列,﹣bn , an , bn+1也成等差数列. (Ⅰ)求证:数列{an+bn}和{an﹣bn}都是等比数列,并求数列{an}的通项公式;
(Ⅱ)若cn=(an﹣3n)log3[an﹣(﹣1)n],求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)的图象上每一点的纵坐标保持不变,横坐标伸长到原来的2倍,再将整个图象沿x轴向右平移 ![]() 个单位,沿y轴向下平移1个单位,得到函数y=
个单位,沿y轴向下平移1个单位,得到函数y= ![]() sinx的图象,则y=f(x)的解析式为( )
sinx的图象,则y=f(x)的解析式为( )
A.y= ![]() sin(2x+
sin(2x+ ![]() )+1
)+1
B.y= ![]() sin(2x﹣
sin(2x﹣ ![]() )+1
)+1
C.y= ![]() sin(
sin( ![]() x+
x+ ![]() )+1
)+1
D.y= ![]() sin(
sin( ![]() x﹣
x﹣ ![]() )+1
)+1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等差数列{an}中,a15+a16+a17=﹣45,a9=﹣36,Sn为其前n项和.
(1)求Sn的最小值,并求出相应的n值;
(2)求Tn=|a1|+|a2|+…+|an|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:m∈{x|x2+(a﹣8)x﹣8a≤0},命题q:方程 ![]() =1表示焦点在x轴上的双曲线.
=1表示焦点在x轴上的双曲线.
(1)若当a=1时,命题p∧q假命题,p∨q”为真命题,求实数m的取值范围;
(2)若命题p是命题q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B是单位圆上的两点,O为圆心,且∠AOB=90°,MN是圆O的一条直径,点C在圆内,且满足 ![]() =λ
=λ ![]() +(1﹣λ)
+(1﹣λ) ![]() (λ∈R),则
(λ∈R),则 ![]()
![]() 的最小值为( )
的最小值为( )
A.﹣ ![]()
B.﹣ ![]()
C.﹣ ![]()
D.﹣1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(其中 ![]() )的图象如图所示,为了得到g(x)=sin2x的图象,则只需将f(x)的图象( )
)的图象如图所示,为了得到g(x)=sin2x的图象,则只需将f(x)的图象( ) 
A.向右平移 ![]() 个长度单位
个长度单位
B.向右平移 ![]() 个长度单位
个长度单位
C.向左平移 ![]() 个长度单位
个长度单位
D.向左平移 ![]() 个长度单位
个长度单位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com