
【题目】函数f(x)=Asin(ωx+φ)(其中 ![]() )的图象如图所示,为了得到g(x)=sin2x的图象,则只需将f(x)的图象( )
)的图象如图所示,为了得到g(x)=sin2x的图象,则只需将f(x)的图象( ) 
A.向右平移 ![]() 个长度单位
个长度单位
B.向右平移 ![]() 个长度单位
个长度单位
C.向左平移 ![]() 个长度单位
个长度单位
D.向左平移 ![]() 个长度单位
个长度单位
【答案】A
【解析】解:由已知中函数f(x)=Asin(ωx+φ)(其中 ![]() )的图象, 过(
)的图象, 过( ![]() ,0)点,(
,0)点,( ![]() )点,
)点,
易得:A=1,T=4( ![]() )=π,即ω=2
)=π,即ω=2
即f(x)=sin(2x+φ),将( ![]() )点代入得:
)点代入得:![]() +φ=
+φ= ![]() +2kπ,k∈Z又由
+2kπ,k∈Z又由 ![]()
∴φ= ![]()
∴f(x)=sin(2x+ ![]() ),
),
设将函数f(x)的图象向左平移a个单位得到函数g(x)=sin2x的图象,
则2(x+a)+ ![]() =2x
=2x
解得a=﹣ ![]()
故将函数f(x)的图象向右平移 ![]() 个长度单位得到函数g(x)=sin2x的图象,
个长度单位得到函数g(x)=sin2x的图象,
故选A
由已知中函数f(x)=Asin(ωx+φ)的图象,我们易分析出函数的周期、最值,进而求出函数f(x)=Asin(ωx+φ)的解析式,设出平移量a后,根据平移法则,我们可以构造一个关于平移量a的方程,解方程即可得到结论.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知 ![]() =(2cosx,sinx﹣cosx),
=(2cosx,sinx﹣cosx), ![]() =(
=( ![]() sinx,sinx+cosx),记函数f(x)=
sinx,sinx+cosx),记函数f(x)= ![]()
![]() . (Ⅰ)求f(x)的表达式,以及f(x)取最大值时x的取值集合;
. (Ⅰ)求f(x)的表达式,以及f(x)取最大值时x的取值集合;
(Ⅱ)设△ABC三内角A,B,C的对应边分别为a,b,c,若a+b=2 ![]() ,c=
,c= ![]() ,f(C)=2,求△ABC的面积.
,f(C)=2,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,平面A1BC⊥侧面A1B1BA,且AA1=AB=BC=2,则AC与平面A1BC所成角为( ) 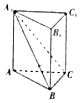
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C所对的边分别为a、b、c,设向量 ![]() =(a,c),
=(a,c), ![]() =(cosC,cosA).
=(cosC,cosA).
(1)若 ![]() ∥
∥ ![]() ,a=
,a= ![]() c,求角A;
c,求角A;
(2)若 ![]()
![]() =3bsinB,cosA=
=3bsinB,cosA= ![]() ,求cosC的值.
,求cosC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在无重复数字的五位数a1a2a3a4a5中,若a1<a2 , a2>a3 , a3<a4 , a4>a5时称为波形数,如89674就是一个波形数,由1,2,3,4,5组成一个没有重复数字的五位数是波形数的概率是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且 ![]() asinA=(
asinA=( ![]() b﹣c)sinB+(
b﹣c)sinB+( ![]() c﹣b)sinC.
c﹣b)sinC.
(1)求角A的大小;
(2)若a= ![]() ,cosB=
,cosB= ![]() ,D为AC的中点,求BD的长.
,D为AC的中点,求BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com