
【题目】已知函数![]() .
.
(Ⅰ)讨论![]() 的单调性;
的单调性;
(Ⅱ)设![]() ,证明:当
,证明:当![]() 时,
时,![]() ;
;
(Ⅲ)设![]() 是
是![]() 的两个零点,证明
的两个零点,证明![]() .
.
【答案】(Ⅰ)![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;(Ⅱ)当
上单调递增;(Ⅱ)当![]() 时,
时,![]() ;(Ⅲ)证明过程见解析
;(Ⅲ)证明过程见解析
【解析】试题分析:(Ⅰ)求导,并判断导数的符号,分别讨论![]() 的取值,确定函数的单调区间.
的取值,确定函数的单调区间.
(Ⅱ)构造函数![]() ,利用导数求函数
,利用导数求函数![]() 当
当![]() 时的最大值小于零即可.
时的最大值小于零即可.
(Ⅲ)由(Ⅱ)得![]() ,从而
,从而![]() ,于是
,于是![]() ,由(Ⅰ)知,
,由(Ⅰ)知,![]() .
.
试题解析:(Ⅰ)![]() 的定义域为
的定义域为![]() ,
,
求导数,得![]() ,
,
若![]() ,则
,则![]() ,此时
,此时![]() 在
在![]() 上单调递增,
上单调递增,
若![]() ,则由
,则由![]() 得
得![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
此时![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(Ⅱ)令![]() ,则
,则
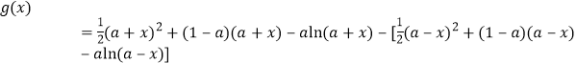
![]() .
.
求导数,得![]() ,
,
当时![]() ,
,![]() ,
,![]() 在
在![]() 上是减函数.
上是减函数.
而![]() ,
,![]() ,
,
故当![]() 时,
时,![]()
(Ⅲ)由(Ⅰ)可知,当![]() 时,函数
时,函数![]() 至多有一个零点,
至多有一个零点,
故![]() ,从而
,从而![]() 的最小值为
的最小值为![]() ,且
,且![]() ,
,
不妨设![]() ,则
,则![]() ,
,![]() ,
,
由(Ⅱ)得![]() ,
,
从而![]() ,于是
,于是![]() ,
,
由(Ⅰ)知,![]() .
.
点晴:本题考查函数导数的单调性.不等式比较大小,函数的零点问题:在(Ⅰ)中通过求导,并判断导数的符号,分别讨论![]() 的取值,确定函数的单调区间.(Ⅱ)通过构造函数
的取值,确定函数的单调区间.(Ⅱ)通过构造函数![]() ,把不等式证明问题转化为函数求最值问题,求函数
,把不等式证明问题转化为函数求最值问题,求函数![]() 当
当![]() 时的最大值小于零即可.(Ⅲ)要充分利用(Ⅰ)(Ⅱ)问的结论.
时的最大值小于零即可.(Ⅲ)要充分利用(Ⅰ)(Ⅱ)问的结论.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() 为自然对数的底数.
为自然对数的底数.
(I)若曲线![]() 在点
在点![]() 处的切线平行于
处的切线平行于![]() 轴,求
轴,求![]() 的值;
的值;
(II)求函数![]() 的极值;
的极值;
(III)当![]() 时,若直线
时,若直线![]() 与曲线
与曲线![]() 没有公共点,求
没有公共点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两队参加听歌猜歌名游戏,每队3人.随机播放一首歌曲,参赛者开始抢答,每人只有一次抢答机会(每人抢答机会均等),答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为 ![]() ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为 ![]() ,
, ![]() ,
, ![]() ,且各人回答正确与否相互之间没有影响.
,且各人回答正确与否相互之间没有影响.
(Ⅰ)若比赛前随机从两队的6个选手中抽取两名选手进行示范,求抽到的两名选手在同一个队的概率;
(Ⅱ)用ξ表示甲队的总得分,求随机变量ξ的分布列和数学期望;
(Ⅲ)求两队得分之和大于4的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)满足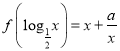 为常数
为常数
(1)求函数f(x)的表达式;
(2)如果f(x)为偶函数,求a的值;
(3)当f(x)为偶函数时,若方程f(x)=m有两个实数根x1,x2;其中x1<0,0<x2<1;求实数m的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下三个命题 ①设回归方程为 ![]() =3﹣3x,则变量x增加一个单位时,y平均增加3个单位;
=3﹣3x,则变量x增加一个单位时,y平均增加3个单位;
②两个随机变量的线性相关性越强,则相关系数的绝对值越接近于1;
③在某项测量中,测量结果ξ服从正态分布N (1,σ2) (σ>0).若ξ在(0,1)内取值的概率为0.4,则ξ在(0,2)内取值的概率为0.8.
其中真命题的个数为( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)对一切实数x,y均有f(x+y)﹣f(y)=(x+2y+2)x成立,且f(2)=12.
(1)求f(0)的值;
(2)在(1,4)上存在x0∈R,使得f(x0)﹣8=ax0成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古代中国数学辉煌灿烂,在《张丘建算经》中记载:“今有十等人,大官甲等十人官赐金,以等次差降之.上三人先入,得金四斤持出;下四人后入,得金三斤持出;中央三人未到者,亦依等次更给.问:各得金几何及未到三人复应得金几何?”则该问题中未到三人共得金多少斤?( )
A.![]()
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①函数y=|x|与函数y=( ![]() )2表示同一个函数;
)2表示同一个函数;
②奇函数的图象一定通过直角坐标系的原点;
③函数y=3(x﹣1)2的图象可由y=3x2的图象向右平移1个单位得到;
④y=2|x|的最小值为1
⑤对于函数f(x),若f(﹣1)f(3)<0,则方程f(x)=0在区间[﹣1,3]上有一实根;
其中正确命题的序号是(填上所有正确命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com