分析:(I)根据题意,直线l
1、l
2方程为x-y-a+b=0、x+y-a-b=0.由两圆半径相等且|AB|=|CD|,得到两圆圆心O
1、O
2到直线l
1、l
2的距离相等,根据点到直线的距离公式建立关于a、b的等式,化简即得a、b所满足的约束条件;
(II)根据直线的斜率公式,得k=
表示点P与原点连线的斜率,所以
=-1+
,由(I)的结论得到k
2∈(
,+∞),代入即可得到
∈(-1,-
).最后根据a=0时
=-1,即得
的取值范围是
[-1,-).
解答:解:(1)∵圆
O1:(x+2)2+(y-2)2=2和圆
O2:(x-3)2+(y-4)2=2的
圆心分别为O
1(-2,2)、O
2(3,4),半径都等于
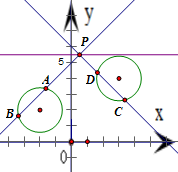
∴当且仅当O
1、O
2到直线l
1、l
2的距离相等时,|AB|=|CD|.
设直线l
1方程为x-y-a+b=0,直线l
2方程为x+y-a-b=0
可得
=
,即|a-b+4|=|a+b-7|
化简得a-b+4=a+b-7或a-b+4=-(a+b-7)
即b=
或a=
∵直线l
1、l
2分别与圆O
1、O
2相交,可得
<且
<,即|a-b+4|<2且|a+b-7|<2
∴当b=
时,-
<a
<; 当a=
时,
<b<
可得a、b所满足的约束条件为:b=
(-
<a
<),a=
(
<b<
)
(II)设k=
表示点P与原点连线的斜率,
可得当b=
,-
<a
<时,k∈(-∞,-11)∪(
,+∞);
当a=
,
<b<
时,k∈(
,5)
∴k
2∈(
,+∞)
∵
=
=-1+
,∴
∈(-1,-
)
结合当a=0,b=
时,
=-1,得
的取值范围是
[-1,-).
点评:本题给出经过点P的两条垂直直线被两圆截得的弦长相等,求点P坐标满足的约束条件,并依此求一个式子的值域.着重考查了直线与圆的位置关系、斜率公式和函数值域的求法等知识,属于中档题.




 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案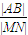 +
+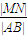 的最大值是 .
的最大值是 .