
【题目】如图所示,在著名的汉诺塔问题中,有三根高度相同的柱子和一些大小及颜色各不相同的圆盘,三根柱子分别为起始柱、辅助柱及目标柱.已知起始柱上套有![]() 个圆盘,较大的圆盘都在较小的圆盘下面.现把圆盘从起始柱全部移到目标柱上,规则如下:每次只能移动一个圆盘,且每次移动后,每根柱上较大的圆盘不能放在较小的圆盘上面,规定一个圆盘从任一根柱上移动到另一根柱上为一次移动.若将
个圆盘,较大的圆盘都在较小的圆盘下面.现把圆盘从起始柱全部移到目标柱上,规则如下:每次只能移动一个圆盘,且每次移动后,每根柱上较大的圆盘不能放在较小的圆盘上面,规定一个圆盘从任一根柱上移动到另一根柱上为一次移动.若将![]() 个圆盘从起始柱移动到目标柱上最少需要移动的次数记为
个圆盘从起始柱移动到目标柱上最少需要移动的次数记为![]() ,则
,则![]() __________,
__________,![]() __________.
__________.
![]()
![]()
【答案】![]()
![]()
【解析】
根据移动方法和规律发现,随着盘子的数目的增多,都是分两个阶段移动,用盘子数目减1的移动次数都移动辅助柱上,然后把最大的盘子移动到目标柱上,再用同样的次数从辅助柱移动到目标柱,从而完成,然后根据移动次数的数据找出总的规律求解.
将![]() 个圆盘从起始柱移动到目标柱上最少需要移动的次数记为
个圆盘从起始柱移动到目标柱上最少需要移动的次数记为![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,小盘移动到辅助柱,大盘移动到目标柱,小盘从辅助柱移动到目标柱,完成,所以
时,小盘移动到辅助柱,大盘移动到目标柱,小盘从辅助柱移动到目标柱,完成,所以![]() ,
,
当![]() 时,小盘移动到目标柱,中盘移动到辅助柱,小盘从目标柱移动辅助柱,即用
时,小盘移动到目标柱,中盘移动到辅助柱,小盘从目标柱移动辅助柱,即用![]() 种方法把中,小盘移动到辅助柱,然后大盘从起始柱移动到目标柱,再用
种方法把中,小盘移动到辅助柱,然后大盘从起始柱移动到目标柱,再用![]() 种方法把中,小盘从辅助柱移动到目标柱.
种方法把中,小盘从辅助柱移动到目标柱.
所以![]()
![]() 的方法,
的方法,
依次类推![]() ,
,![]() ,
,
故答案为:(1). ![]() (2).
(2). ![]()


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:
【题目】如图,![]() 三个警亭有直道相通,已知
三个警亭有直道相通,已知![]() 在
在![]() 的正北方向6千米处,
的正北方向6千米处,![]() 在
在![]() 的正东方向
的正东方向![]() 千米处.
千米处.
(1)警员甲从![]() 出发,沿
出发,沿![]() 行至点
行至点![]() 处,此时
处,此时![]() ,求
,求![]() 的距离;
的距离;
(2)警员甲从![]() 出发沿
出发沿![]() 前往
前往![]() ,警员乙从
,警员乙从![]() 出发沿
出发沿![]() 前往
前往![]() ,两人同时出发,甲的速度为3千米/小时,乙的速度为6千米/小时.两人通过专用对讲机保持联系,乙到达
,两人同时出发,甲的速度为3千米/小时,乙的速度为6千米/小时.两人通过专用对讲机保持联系,乙到达![]() 后原地等待,直到甲到达
后原地等待,直到甲到达![]() 时任务结束.若对讲机的有效通话距离不超过9千米,试问两人通过对讲机能保持联系的总时长?
时任务结束.若对讲机的有效通话距离不超过9千米,试问两人通过对讲机能保持联系的总时长?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() (a>b>0)的离心率
(a>b>0)的离心率![]() ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为![]() .
.
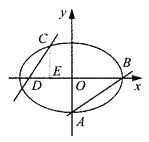
(1)求椭圆的方程.
(2)已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象与
的图象与![]() 轴的交点中,相邻两个交点之间的距离为
轴的交点中,相邻两个交点之间的距离为![]() ,且图象过点
,且图象过点![]()
(1)求![]() 的解析式;
的解析式;
(2)求函数![]() 的单调递增区间;
的单调递增区间;
(3)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数
个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数![]() 的图象,若关于
的图象,若关于![]() 的方程
的方程![]() ,在区间
,在区间![]() 上有且只有一个实数解,求实数
上有且只有一个实数解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某品种一批树苗生长情况,在该批树苗中随机抽取了容量为120的样本,测量树苗高度(单位:cm),经统计,其高度均在区间[19,31]内,将其按[19,21),[21,23),[23,25),[25,27),[27,29),[29,31]分成6组,制成如图所示的频率分布直方图.其中高度为27 cm及以上的树苗为优质树苗.
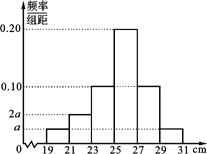
(1)求图中a的值;
(2)已知所抽取的这120棵树苗来自于A,B两个试验区,部分数据如下列联表:
A试验区 | B试验区 | 合计 | |
优质树苗 | 20 | ||
非优质树苗 | 60 | ||
合计 |
将列联表补充完整,并判断是否有99.9%的把握认为优质树苗与A,B两个试验区有关系,并说明理由;
(3)用样本估计总体,若从这批树苗中随机抽取4棵,其中优质树苗的棵数为X,求X的分布列和数学期望EX.
下面的临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某地一天从![]() 时的温度变化曲线近似满足函数
时的温度变化曲线近似满足函数![]() .
.
(1)求该地区这一段时间内温度的最大温差.
(2)若有一种细菌在![]() 到
到![]() 之间可以生存,则在这段时间内,该细菌最多能存活多长时间?
之间可以生存,则在这段时间内,该细菌最多能存活多长时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com