
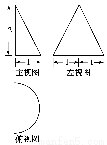
某几何体的三视图如图所示,则其体积为________.
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)仿真模拟卷1练习卷(解析版) 题型:解答题
如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD为矩形,E为PD上一点,AD=2AB=2AP=2,PE=2DE.
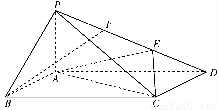
(1)若F为PE的中点,求证:BF∥平面ACE;
(2)求三棱锥P-ACE的体积.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷5练习卷(解析版) 题型:解答题
已知椭圆E: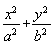 =1(a>b>0),F1(-c,0),F2(c,0)为椭圆的两个焦点,M为椭圆上任意一点,且|MF1|,|F1F2|,|MF2|构成等差数列,点F2(c,0)到直线l:x=
=1(a>b>0),F1(-c,0),F2(c,0)为椭圆的两个焦点,M为椭圆上任意一点,且|MF1|,|F1F2|,|MF2|构成等差数列,点F2(c,0)到直线l:x=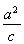 的距离为3.
的距离为3.
(1)求椭圆E的方程;
(2)若存在以原点为圆心的圆,使该圆的任意一条切线与椭圆E恒有两个交点A,B,且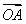 ⊥
⊥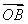 ,求出该圆的方程.
,求出该圆的方程.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷5练习卷(解析版) 题型:选择题
已知点M(a,b)在圆O:x2+y2=1外,则直线ax+by=1与圆O的位置关系是( )
A.相切 B.相交
C.相离 D.不确定
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷4练习卷(解析版) 题型:解答题
如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,已知PB=PD=2,PA=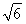 .
.
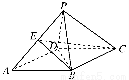
(1)证明:PC⊥BD;
(2)若E为PA的中点,求三棱锥P-BCE的体积.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷4练习卷(解析版) 题型:选择题
设m,n是两条不同的直线,α,β,γ是三个不同的平面,有以下四个命题:
①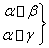 ⇒β∥γ②
⇒β∥γ②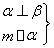 ⇒m⊥β③
⇒m⊥β③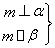 ⇒α⊥β④
⇒α⊥β④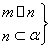 ⇒m∥α
⇒m∥α
其中正确的命题是( )
A.①④ B.②③ C.①③ D.②④
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷3练习卷(解析版) 题型:解答题
在公差为d的等差数列{an}中,已知a1=10,且a1,2a2+2,5a3成等比数列.
(1)求d,an;
(2)若d<0,求|a1|+|a2|+|a3|+…+|an|.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷3练习卷(解析版) 题型:选择题
在数列{an}中,a1=2i(i为虚数单位),(1+i)an+1=(1-i)an(n∈N*),则a2 012的值为( )
A.-2 B.0 C.2 D.2i
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(解析版) 题型:选择题
已知e1,e2是两个单位向量,其夹角为θ,若向量m=2e1+3e2,则|m|=1的充要条件是( )
A.θ=π B.θ=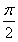
C.θ=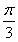 D.θ=
D.θ=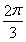
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com