
在公差为d的等差数列{an}中,已知a1=10,且a1,2a2+2,5a3成等比数列.
(1)求d,an;
(2)若d<0,求|a1|+|a2|+|a3|+…+|an|.
(1)an=-n+11(n∈N*)或an=4n+6(n∈N*)(2)
【解析】(1)由题意得,a1·5a3=(2a2+2)2,由a1=10,{an}为公差为d的等差数列得,d2-3d-4=0,解得d=-1或d=4.所以an=-n+11(n∈N*)或an=4n+6(n∈N*).
(2)设数列{an}的前n项和为Sn.
因为d<0,由(1)得d=-1,an=-n+11,
所以当n≤11时,|a1|+|a2|+|a3|+…+|an|=Sn=-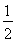 n2+
n2+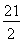 n;
n;
当n≥12时,|a1|+|a2|+|a3|+…+|an|=-Sn+2S11=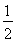 n2-
n2-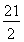 n+110.
n+110.
综上所述,
|a1|+|a2|+|a3|+…+|an|=


科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)仿真模拟卷1练习卷(解析版) 题型:选择题
已知球的半径为5,球面被互相垂直的两个平面所截,得到的两个圆的公共弦长为2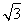 ,若其中一个圆的半径为4,则另一个圆的半径为( )
,若其中一个圆的半径为4,则另一个圆的半径为( )
A.3 B.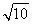 C.
C.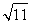 D.2
D.2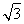
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷5练习卷(解析版) 题型:选择题
已知直线l过抛物线y2=4x的焦点F,交抛物线于A、B两点,且点A、B到y轴的距离分别为m,n,则m+n+2的最小值为( )
A.4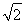 B.6
B.6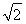 C.4 D.6
C.4 D.6
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷4练习卷(解析版) 题型:选择题
一几何体的三视图如图所示,则该几何体的体积为( )、
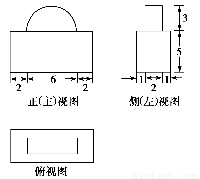
A.200+9π B.200+18π
C.140+9π D.140+18π
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷3练习卷(解析版) 题型:填空题
二维空间中圆的一维测度(周长)l=2πr,二维测度(面积)S=πr2,观察发现S′=l;三维空间中球的二维测度(表面积)S=4πr2,三维测度(体积)V=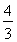 πr3,观察发现V′=S.则由四维空间中“超球”的三维测度V=8πr3,猜想其四维测度W=________.
πr3,观察发现V′=S.则由四维空间中“超球”的三维测度V=8πr3,猜想其四维测度W=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷3练习卷(解析版) 题型:选择题
下列推理中属于归纳推理且结论正确的是( )
A.设数列{an}的前n项和为Sn.由an=2n-1,求出S1=12,S2=22,S3=32,…,推断:Sn=n2
B.由f(x)=xcos x满足f(-x)=-f(x)对?x∈R都成立,推断:f(x)=xcos x为奇函数
C.由圆x2+y2=r2的面积S=πr2,推断:椭圆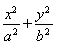 =1(a>b>0)的面积S=πab
=1(a>b>0)的面积S=πab
D.由(1+1)2>21,(2+1)2>22,(3+1)2>23,…,推断:对一切n∈N*,(n+1)2>2n
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练解答题押题练C组练习卷(解析版) 题型:解答题
某创业投资公司拟投资开发某种新能源产品,估计能获得10万元到1 000万元的投资收益.现准备制定一个对科研课题组的奖励方案:资金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.
(1)若建立函数y=f(x)模型制定奖励方案,试用数学语言表述该公司对奖励函数f(x)模型的基本要求,并分析函数y=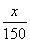 +2是否符合公司要求的奖励函数模型,并说明原因;
+2是否符合公司要求的奖励函数模型,并说明原因;
(2)若该公司采用模型函数y=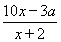 作为奖励函数模型,试确定最小的正整数a的值.
作为奖励函数模型,试确定最小的正整数a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com