
已知直线l过抛物线y2=4x的焦点F,交抛物线于A、B两点,且点A、B到y轴的距离分别为m,n,则m+n+2的最小值为( )
A.4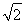 B.6
B.6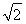 C.4 D.6
C.4 D.6
 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)仿真模拟卷2练习卷(解析版) 题型:填空题
已知F1,F2是双曲线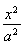 -y2=1的两个焦点,点P在此双曲线上,
-y2=1的两个焦点,点P在此双曲线上,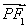 ·
·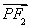 =0,如果点P到x轴的距离等于
=0,如果点P到x轴的距离等于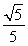 ,那么该双曲线的离心率等于________.
,那么该双曲线的离心率等于________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷6练习卷(解析版) 题型:解答题
已知A、B、C三个箱子中各装有两个完全相同的球,每个箱子里的球,有一个球标着号码1,另一个球标着号码2.现从A、B、C三个箱子中各摸出一个球.
(1)若用数组(x,y,z)中的x、y、z分别表示从A、B、C三个箱子中摸出的球的号码,请写出数组(x,y,z)的所有情形,并回答一共有多少种;
(2)如果请您猜测摸出的这三个球的号码之和,猜中有奖.那么猜什么数获奖的可能性最大?请说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷5练习卷(解析版) 题型:解答题
已知椭圆E: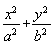 =1(a>b>0),F1(-c,0),F2(c,0)为椭圆的两个焦点,M为椭圆上任意一点,且|MF1|,|F1F2|,|MF2|构成等差数列,点F2(c,0)到直线l:x=
=1(a>b>0),F1(-c,0),F2(c,0)为椭圆的两个焦点,M为椭圆上任意一点,且|MF1|,|F1F2|,|MF2|构成等差数列,点F2(c,0)到直线l:x=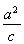 的距离为3.
的距离为3.
(1)求椭圆E的方程;
(2)若存在以原点为圆心的圆,使该圆的任意一条切线与椭圆E恒有两个交点A,B,且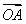 ⊥
⊥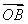 ,求出该圆的方程.
,求出该圆的方程.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷5练习卷(解析版) 题型:填空题
在平面直角坐标系xOy中,椭圆C的中心为原点,焦点F1,F2在x轴上,离心率为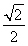 .过F1的直线l交C于A,B两点,且△ABF2的周长为16,那么C的方程为________.
.过F1的直线l交C于A,B两点,且△ABF2的周长为16,那么C的方程为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷5练习卷(解析版) 题型:选择题
已知点M(a,b)在圆O:x2+y2=1外,则直线ax+by=1与圆O的位置关系是( )
A.相切 B.相交
C.相离 D.不确定
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷4练习卷(解析版) 题型:解答题
如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,已知PB=PD=2,PA=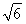 .
.
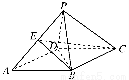
(1)证明:PC⊥BD;
(2)若E为PA的中点,求三棱锥P-BCE的体积.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷3练习卷(解析版) 题型:解答题
在公差为d的等差数列{an}中,已知a1=10,且a1,2a2+2,5a3成等比数列.
(1)求d,an;
(2)若d<0,求|a1|+|a2|+|a3|+…+|an|.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(解析版) 题型:解答题
设函数f(x)=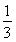 x3-ax2-ax,g(x)=2x2+4x+c.
x3-ax2-ax,g(x)=2x2+4x+c.
(1)试问函数f(x)能否在x=-1时取得极值?说明理由;
(2)若a=-1,当x∈[-3,4]时,函数f(x)与g(x)的图象有两个公共点,求c的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com