
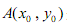 是曲线C上的一个定点,过点A任意作两条倾斜角互补的直线,分别与曲线C相交于另外两点P 、Q.
是曲线C上的一个定点,过点A任意作两条倾斜角互补的直线,分别与曲线C相交于另外两点P 、Q.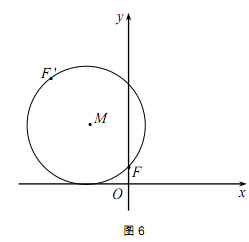
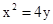 ;(2)见解析.
;(2)见解析.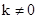 ),则直线AQ的斜率为-k. ………………6分
),则直线AQ的斜率为-k. ………………6分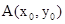 是曲线C:
是曲线C: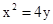 上的点,
上的点,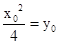 ,直线AP的方程为
,直线AP的方程为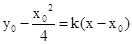 .
.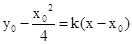 与
与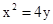 联立,
联立,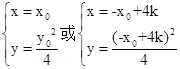 ,
,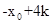 ,
,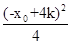 ),
),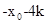 ,
,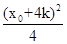 )
)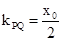 为定值
为定值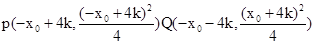 ,,
,,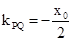 ,所以直线QP的方程为,
,所以直线QP的方程为,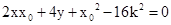 得到B的坐标。
得到B的坐标。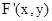 ,因为点
,因为点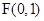 在圆M上,
在圆M上,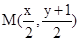 …………1分
…………1分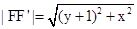 .…………2分
.…………2分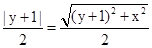 ,两边平方整理得:
,两边平方整理得: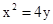 ,
,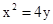 . ………………………………5分
. ………………………………5分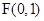 且与x轴相切,所以动圆M在x轴上方,
且与x轴相切,所以动圆M在x轴上方,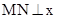 轴,垂足为N,过点F’作
轴,垂足为N,过点F’作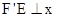 轴,垂足为E(如图6-1).
轴,垂足为E(如图6-1).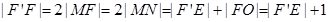 ,
,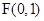 的距离比到
的距离比到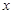 轴的距离大1.……………………………3分
轴的距离大1.……………………………3分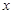 轴的上方(包括
轴的上方(包括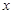 轴上),
轴上),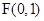 的距离与到定直线y=-1的距离相等.
的距离与到定直线y=-1的距离相等.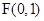 为焦点,以直线y=1为准线的抛物线.
为焦点,以直线y=1为准线的抛物线.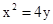 . ……………………………5分
. ……………………………5分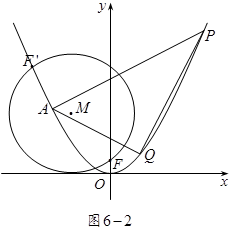
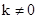 ),则直线AQ的斜率为-k. ………………6分
),则直线AQ的斜率为-k. ………………6分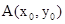 是曲线C:
是曲线C: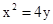 上的点,
上的点,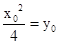 ,直线AP的方程为
,直线AP的方程为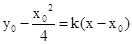 .
.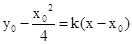 与
与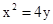 联立,
联立,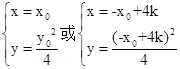 ,
,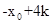 ,
,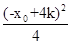 ),
),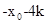 ,
,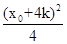 ),. ………………8分
),. ………………8分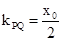 为定值.………………10分
为定值.………………10分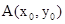 是曲线C:
是曲线C: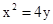 上的点,所以
上的点,所以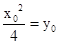 ,
,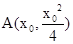
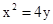 上,所以可设
上,所以可设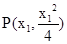 ,
,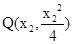 , …6分
, …6分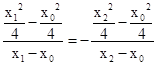 ,整理得
,整理得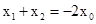 .8分
.8分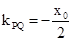 为定值. ………10分
为定值. ………10分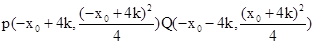 ,
,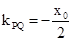 ,所以直线QP的方程为,
,所以直线QP的方程为,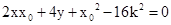 . …………11分
. …………11分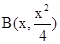 在曲线段l上,因为P、Q两点的横坐标分别为
在曲线段l上,因为P、Q两点的横坐标分别为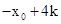 和
和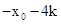 ,
,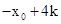 和
和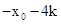 之间,
之间,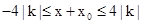 ,从而
,从而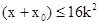 .
.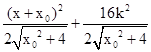 .………12分
.………12分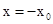 时,d的最大值为
时,d的最大值为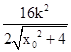 .
.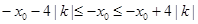 ,所以点
,所以点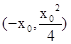 在曲线段L上.
在曲线段L上.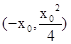 .…………………………………………14分
.…………………………………………14分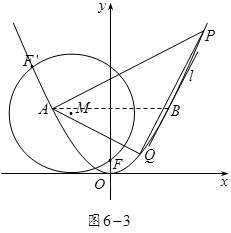
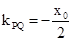 ,结合图6-3可知,
,结合图6-3可知,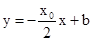 ,由方程组
,由方程组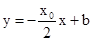
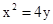 联立可得
联立可得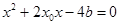 .
.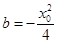 .……12分
.……12分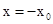 ,
,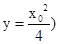 .
.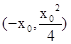 .……………………………………………14分
.……………………………………………14分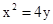 关于y轴对称,
关于y轴对称,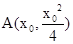 关于
关于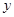 轴的对称点
轴的对称点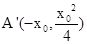 .……11分
.……11分
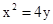 和①的结论,
和①的结论,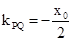 .
.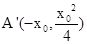 为切点的切线L//PQ.
为切点的切线L//PQ.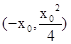 .……………14分
.……………14分

 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源:不详 题型:解答题
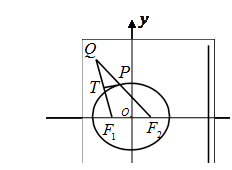
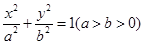 的左、右焦点分别是
的左、右焦点分别是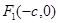 、
、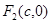 ,离心率为
,离心率为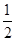 ,椭圆上的动点
,椭圆上的动点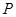 到直线
到直线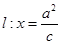 的最小距离为2,延长
的最小距离为2,延长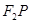 至
至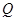 使得
使得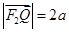 ,线段
,线段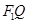 上存在异于
上存在异于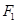 的点
的点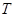 满足
满足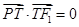 .
.
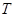 的轨迹
的轨迹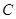 的方程;
的方程;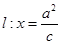 上任意一点必可以作两条直线
上任意一点必可以作两条直线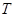 的轨迹
的轨迹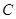 相切,并且过两切点的直线经过定点.
相切,并且过两切点的直线经过定点. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com