
分析 (1)设切线方程为:y=kx,则$\frac{|-2k+2|}{{\sqrt{{k^2}+1}}}=\sqrt{2}$$⇒k=2±\sqrt{3}$,即可求该切线的方程;
(2)题知,∠EQF=$\frac{π}{3}$,即QM=2ME,求出Q的轨迹方程,即可求Q点的坐标;
(3)求出A,B的坐标,利用斜率公式证明kAB=kOP⇒直线OP与AB平行.
解答 解:(1)设切线方程为:y=kx,则$\frac{|-2k+2|}{{\sqrt{{k^2}+1}}}=\sqrt{2}$$⇒k=2±\sqrt{3}$
⇒切线方程为$y=(2+\sqrt{3})x$或$y=(2-\sqrt{3})x$;
(2)由题知,∠EQF=$\frac{π}{3}$,即QM=2ME,设Q(x,y),则Q的轨迹为:$\left\{\begin{array}{l}{(x+2)^2}+{(y+2)^2}=8\\{x^2}+{y^2}=2\end{array}\right.⇒\left\{\begin{array}{l}x=\frac{{3-\sqrt{15}}}{4}\\ y=\frac{{-1+\sqrt{15}}}{4}\end{array}\right.或\left\{\begin{array}{l}x=\frac{{-1+\sqrt{15}}}{4}\\ y=\frac{{-1-\sqrt{15}}}{4}\end{array}\right.$
即$Q(\frac{{-1-\sqrt{15}}}{4},\frac{{-1+\sqrt{15}}}{4})或Q(\frac{{-1+\sqrt{15}}}{4},\frac{{-1-\sqrt{15}}}{4})$
(3)由题设lPA:y-1=k(x-1)则lPB:y-1=-k(x-1)
由$\left\{\begin{array}{l}y-1=k(x-1)\\{x^2}+{y^2}=2\end{array}\right.⇒(1+{k^2}){x^2}+2k(1-k)x+{(1-k)^2}-2=0$$⇒{x_A}=\frac{{{k^2}-2k-1}}{{1+{k^2}}}$;
同理${x_B}=\frac{{{k^2}+2k-1}}{{1+{k^2}}}$$⇒{k_{AB}}=\frac{{{y_B}-{y_A}}}{{{x_B}-{x_A}}}=\frac{{-k({x_A}+{x_B})+2k}}{{{x_B}-{x_A}}}=1$
又kOP=1⇒kAB=kOP⇒直线OP与AB平行.
点评 本题考查轨迹方程,考查直线与圆位置关系的运用,考查斜率的计算,属于中档题.


 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:选择题
 观察如图所示的正方形图案,每条边(包括两个端点)有n(n≥2,n∈N*)个圆点,第n个图案中圆点的总数是Sn.按此规律推断出Sn与n的关系式为( )
观察如图所示的正方形图案,每条边(包括两个端点)有n(n≥2,n∈N*)个圆点,第n个图案中圆点的总数是Sn.按此规律推断出Sn与n的关系式为( )| A. | Sn=2n | B. | Sn=4n | C. | Sn=2n | D. | Sn=4n-4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
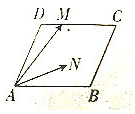 如图,在平行四边形ABCD中,AB=4,AD=2,∠DAB=60°,点M在线段DC上,且满足$\overrightarrow{DM}$=$\frac{1}{4}$$\overrightarrow{DC}$,若N是平行四边形ABCD内的任意一点(含边界),则$\overrightarrow{AM}•\overrightarrow{AN}$的取值范围是[0,13].
如图,在平行四边形ABCD中,AB=4,AD=2,∠DAB=60°,点M在线段DC上,且满足$\overrightarrow{DM}$=$\frac{1}{4}$$\overrightarrow{DC}$,若N是平行四边形ABCD内的任意一点(含边界),则$\overrightarrow{AM}•\overrightarrow{AN}$的取值范围是[0,13].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2] | B. | [4,+∞) | C. | (-∞,2] | D. | (0,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$ | B. | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AC}$ | C. | $\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$ | D. | $\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$-$\frac{1}{3}$$\overrightarrow{AC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,将正六边形ABCDEF中的一半图形ABCD绕AD翻折到AB1C1D,使得∠B1AF=60°.G是BF与AD的交点.
如图,将正六边形ABCDEF中的一半图形ABCD绕AD翻折到AB1C1D,使得∠B1AF=60°.G是BF与AD的交点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com