Question

1．如图，将正六边形ABCDEF中的一半图形ABCD绕AD翻折到AB₁C₁D，使得∠B₁AF=60°．G是BF与AD的交点．
（Ⅰ）求证：平面ADEF⊥平面B₁FG；
（Ⅱ）求直线AB₁与平面ADEF所成角的正弦值．

Answer 1

分析 （Ⅰ）推导出B₁G⊥AD，FG⊥AD，从而AD⊥平面B₁GF，由此能证明平面ADEF⊥平面B₁FG．
（Ⅱ）法一：作B₁H⊥FG于H，连接AH，则∠B₁AH就是直线B₁A与平面ADEF所成的角，由此能求出直线AB₁与平面ADEF所成角的正弦值．
法二：以A为坐标原点，以AD为x轴，过A在平面ADEF内作垂直于AD的直线为y轴，过A作垂直于平面ADEF的直线为z轴建立空间直角坐标系，利用向量法能求出直线AB₁与平面ADEF所成角的正弦值为$\frac{{\sqrt{6}}}{3}$．

解答 证明：（Ⅰ）由正六边形对称性可知BF⊥AD，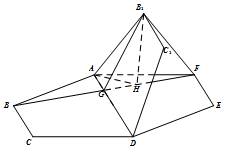
因此B₁G⊥AD，FG⊥AD．   …．（3分）
又B₁G∩FG=G，B₁G?平面B₁GF，FG?平面B₁GF，
所以AD⊥平面B₁GF． …．（5分）
又因为AD?平面ADEF，
所以平面ADEF⊥平面B₁FG．…．（7分）
（Ⅱ）（方法一）由（Ⅰ）已得平面B₁GF⊥平面ADEF．
作B₁H⊥FG于H，
又由于平面B₁GF∩平面ADEF=FG，
所以B₁H⊥平面ADEF．
连接AH，则∠B₁AH就是直线B₁A与平面ADEF所成的角．  …．（11分）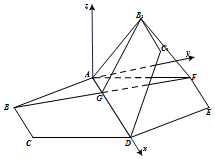
不妨设正六边形边长为2．
则AF=AB₁=2且∠B₁AF=60°，∠B₁AG=∠FAG=60°
得B₁F=2，${B_1}G=FG=\sqrt{3}$．
在△B₁GF中，$cos∠{B_1}GF=\frac{{{B_1}{G^2}+G{F^2}-{B_1}{F^2}}}{{2{B_1}G•GF}}$=$\frac{{{{\sqrt{3}}^2}+{{\sqrt{3}}^2}-{2^2}}}{{2×\sqrt{3×\sqrt{3}}}}=\frac{1}{3}$．
$sin∠{B_1}GH=\frac{{2\sqrt{2}}}{3}$．${B_1}H={B_1}G•sin∠{B_1}GH=\frac{{2\sqrt{6}}}{3}$，
$sin∠{B_1}AH=\frac{{{B_1}H}}{{{B_1}A}}=\frac{{\sqrt{6}}}{3}$，
所以直线AB₁与平面ADEF所成角的正弦值为$\frac{{\sqrt{6}}}{3}$．   …．（15分）
（方法二）如图，以A为坐标原点，以AD为x轴，
过A在平面ADEF内作垂直于AD的直线为y轴，
过A作垂直于平面ADEF的直线为z轴建立空间直角坐标系．
不妨设正六边形边长为2．则$\overrightarrow{AD}=（4，0，0）$，$\overrightarrow{AF}=（1，\sqrt{3}，0）$，
设$\overrightarrow{A{B_1}}=（x，y，z）$．
由$\frac{{\overrightarrow{A{B_1}}•\overrightarrow{AD}}}{{|\overrightarrow{A{B_1}}|•|\overrightarrow{AD}|}}=\frac{x×4}{2×4}=cos60°=\frac{1}{2}$
得x①．
由$\frac{{\overrightarrow{A{B_1}}•\overrightarrow{AF}}}{{|\overrightarrow{A{B_1}}|•|\overrightarrow{AF}|}}=\frac{{x+\sqrt{3}y}}{2×2}=cos60°=\frac{1}{2}$得$x+\sqrt{3}y=2$②．
又${（\overrightarrow{A{B_1}}）^2}={x^2}+{y^2}+{z^2}=4$③．…．（10分）
由①②③得$x=4，y=\frac{1}{{\sqrt{3}}}，z=\frac{{2\sqrt{2}}}{{\sqrt{3}}}$．所以$\overrightarrow{A{B_1}}=（1，\frac{1}{{\sqrt{3}}}，\frac{{2\sqrt{2}}}{{\sqrt{3}}}）$． …．（13分）
取平面ADEF的法向量$\overrightarrow n=（0，0，1）$．$cos\left?{\overrightarrow{A{B_1}}，\overrightarrow n}\right＞=\frac{{\overrightarrow{A{B_1}}•\overrightarrow n}}{{|\overrightarrow{A{B_1}}|•|\overrightarrow n|}}=\frac{{\sqrt{6}}}{3}$．
所以直线AB₁与平面ADEF所成角的正弦值为$\frac{{\sqrt{6}}}{3}$．           …．（15分）

点评 本题考查面面垂直的证明，考查线面角的正弦值的求法，考查空间中线线、线面、面面的位置关系等基础知识，考查推理论证能力、数据处理能力、空间想象能力，考查化归与转化思想、数形结合思想，是中档题．