
| A. | (-2,2) | B. | $(-\frac{5}{2},\frac{5}{2})$ | C. | $(-\frac{5}{2},-1)∪(1,\frac{5}{2})$ | D. | $(-∞,-\frac{5}{2})∪(\frac{5}{2},+∞)$ |
分析 根据题意,将函数f(x)写成分段函数的形式为f(x)=$\left\{\begin{array}{l}{x+{x}^{2},x≥0}\\{xx-{x}^{2},x<0}\end{array}\right.$,进而分析可得函数f(x)为增函数,则可以将f(x2+1)>f(ax)转化为x2+1>ax,即不等式x2+1>ax的解集为A,结合题意可得$\left\{\begin{array}{l}{(-\frac{1}{2})^{2}+1>(-\frac{1}{2})×a}\\{(\frac{1}{2})^{2}+1>(\frac{1}{2})×a}\end{array}\right.$,解可得a的取值范围,即可得答案.
解答 解:根据题意,f(x)=x(1+|x|)=$\left\{\begin{array}{l}{x+{x}^{2},x≥0}\\{xx-{x}^{2},x<0}\end{array}\right.$,
分析可得:函数f(x)为增函数,
若f(x2+1)>f(ax)的解集为A,则不等式x2+1>ax的解集为A,
又由$[-\frac{1}{2},\frac{1}{2}]⊆A$,
则有$\left\{\begin{array}{l}{(-\frac{1}{2})^{2}+1>(-\frac{1}{2})×a}\\{(\frac{1}{2})^{2}+1>(\frac{1}{2})×a}\end{array}\right.$,
解可得-$\frac{5}{2}$<a<$\frac{5}{2}$,
即a的取值范围是(-$\frac{5}{2}$,$\frac{5}{2}$);
故选:B.
点评 本题考查分段函数的应用,涉及函数单调性的应用,关键要将函数写成分段函数的形式,再分析函数的单调性.


科目:高中数学 来源: 题型:填空题
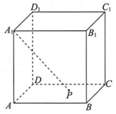 如图,正方体ABCD-A1B1C1D1的棱长为2,点P在正方形ABCD的边界及其内部运动.平面区域W由所有满足A1P≥$\sqrt{5}$的点P组成,则W的面积是$\frac{π}{4}$.
如图,正方体ABCD-A1B1C1D1的棱长为2,点P在正方形ABCD的边界及其内部运动.平面区域W由所有满足A1P≥$\sqrt{5}$的点P组成,则W的面积是$\frac{π}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{12}{25}$ | B. | $-\frac{12}{25}$ | C. | $\frac{24}{25}$ | D. | $-\frac{24}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,将正六边形ABCDEF中的一半图形ABCD绕AD翻折到AB1C1D,使得∠B1AF=60°.G是BF与AD的交点.
如图,将正六边形ABCDEF中的一半图形ABCD绕AD翻折到AB1C1D,使得∠B1AF=60°.G是BF与AD的交点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 可以不存在 | B. | 至少有1个 | C. | 至少有2个 | D. | 至多有2个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
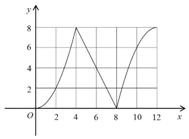 如图,函数f(x)的图象经过(0,0),(4,8),(8,0),(12,8)四个点,试用“>,=,<”填空:
如图,函数f(x)的图象经过(0,0),(4,8),(8,0),(12,8)四个点,试用“>,=,<”填空:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com