
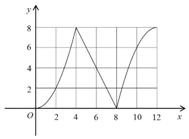
 如图,函数f(x)的图象经过(0,0),(4,8),(8,0),(12,8)四个点,试用“>,=,<”填空:
如图,函数f(x)的图象经过(0,0),(4,8),(8,0),(12,8)四个点,试用“>,=,<”填空:分析 (1)代入函数值计算或根据平均变化率的几何意义比较割线的斜率;
(2)根据导数的几何意义比较切线的斜率即可.
解答 解:(1)由函数图象可知$\frac{f(4)-f(2)}{2}$=$\frac{6}{2}=3$,$\frac{f(12)-f(8)}{4}$=$\frac{8}{4}$=2,
∴$\frac{f(4)-f(2)}{2}>\frac{f(12)-f(8)}{4}$.
(2)∵f(x)在(4,8)上是减函数,在(8,12)上是增函数,
∴f′(6)<0,f′(10)>0,
∴f′(6)<f′(10).
故答案为(1)>,(2)<.
点评 本题考查了导数的几何意义,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,2) | B. | $(-\frac{5}{2},\frac{5}{2})$ | C. | $(-\frac{5}{2},-1)∪(1,\frac{5}{2})$ | D. | $(-∞,-\frac{5}{2})∪(\frac{5}{2},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
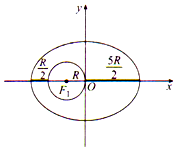 我国自主研制的第一个月球探测器--“嫦娥一号”卫星在西昌卫星发射中心成功发射后,在地球轨道上经历3次调相轨道变轨,奔向月球,进入月球轨道,“嫦娥一号”轨道是以地心为一个焦点的椭圆,设地球半径为R,卫星近地点,远地点离地面的距离分别是$\frac{R}{2}$,$\frac{5R}{2}$(如图所示),则“嫦娥一号”卫星轨道的离心率为( )
我国自主研制的第一个月球探测器--“嫦娥一号”卫星在西昌卫星发射中心成功发射后,在地球轨道上经历3次调相轨道变轨,奔向月球,进入月球轨道,“嫦娥一号”轨道是以地心为一个焦点的椭圆,设地球半径为R,卫星近地点,远地点离地面的距离分别是$\frac{R}{2}$,$\frac{5R}{2}$(如图所示),则“嫦娥一号”卫星轨道的离心率为( )| A. | $\frac{2}{5}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+i | B. | -1+i | C. | 1-i | D. | -1-i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com