
分析 (1)由a3+a5=a4+7,S10=100,列出方程组,求出首项和公差,由此能求出{an}的通项公式.
(2)由a1=1,an=2n-1,求出Sn=n2,从而得到n2-6n+5<0,由此能求出n的值.
解答 (本题10分)
解:(1)设数列{an}的公差为d,
由a3+a5=a4+7,得2a1+6d=a1+3d+7,①.…(1分)
由S10=100,得10a1+45d=100,②…(2分)
解得a1=1,d=2,…(4分)
所以an=a1+(n-1)d=2n-1.…(5分)
(2)因为a1=1,an=2n-1,所以${S}_{n}=\frac{n({a}_{1}+{a}_{n})}{2}$=n2,…(7分)
由不等式Sn<3an-2,得n2<3(2n-1)-2,
所以,n2-6n+5<0,
解得1<n<5,…(9分)
因为n∈N*,
所以n的值为2,3,4.…(10分)
点评 本题考查等差数列的通项公式、项数n的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
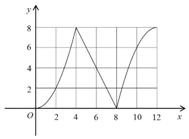 如图,函数f(x)的图象经过(0,0),(4,8),(8,0),(12,8)四个点,试用“>,=,<”填空:
如图,函数f(x)的图象经过(0,0),(4,8),(8,0),(12,8)四个点,试用“>,=,<”填空:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com