
已知函数, .
.
(1)求曲线f(x)在点A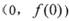 处的切线方程;
处的切线方程;
(II)讨论函数f(x)的单调性;
(III)是否存在实数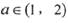 ,使
,使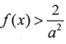 当
当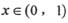 时恒成立?若存在,求 出实数a;若不存在,请说明理由
时恒成立?若存在,求 出实数a;若不存在,请说明理由
(Ⅰ)∵ a>0,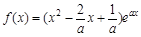 ,
,
∴ 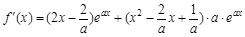
=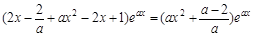 ,
…… 2分
,
…… 2分
于是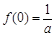 ,
, ,所以曲线y = f(x)在点A(0,f(0))处的切线方程为
,所以曲线y = f(x)在点A(0,f(0))处的切线方程为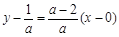 ,即(a-2)x-ay + 1 = 0.
……… 4分
,即(a-2)x-ay + 1 = 0.
……… 4分
(Ⅱ)∵ a>0,eax>0,∴ 只需讨论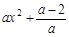 的符号. ………… 5分
的符号. ………… 5分
ⅰ)当a>2时,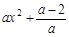 >0,这时f ′(x)>0,所以函数f(x)在(-∞,+∞)上为增函数.
>0,这时f ′(x)>0,所以函数f(x)在(-∞,+∞)上为增函数.
ⅱ)当a = 2时,f ′(x)= 2x2e2x≥0,函数f(x)在(-∞,+∞)上为增函数.…6分
ⅲ)当0<a<2时,令f ′(x)= 0,解得 ,
,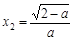 .
.
当x变化时, f '(x)和f(x)的变化情况如下表:
|
x |
|
|
|
|
|
|
f '(x) |
+ |
0 |
- |
0 |
+ |
|
f(x) |
↗ |
极大值 |
↘ |
极小值 |
↗ |
∴f(x)在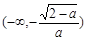 ,
,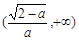 ,为增函数,f(x)在
,为增函数,f(x)在 为减函数. …… 9分
为减函数. …… 9分
(Ⅲ)当a∈(1,2)时,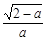 ∈(0,1).由(Ⅱ)知f(x)在
∈(0,1).由(Ⅱ)知f(x)在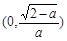 上是减函数,在
上是减函数,在 上是增函数,故当x∈(0,1)时,
上是增函数,故当x∈(0,1)时, ,……10分
,……10分
∴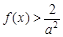 当x∈(0,1)时恒成立,等价于
当x∈(0,1)时恒成立,等价于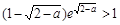 恒成立.……11分
恒成立.……11分
当a∈(1,2)时,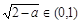 ,设
,设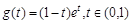 ,则
,则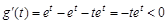 ,表明g(t) 在(0,1)上单调递减,于是可得
,表明g(t) 在(0,1)上单调递减,于是可得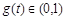 ,即a∈(1,2)时
,即a∈(1,2)时 恒成立,……13分 符合条件的实数a不存在.
恒成立,……13分 符合条件的实数a不存在.
【解析】略


科目:高中数学 来源: 题型:
| a |
| x |
| lnx |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| x |
| 3 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com