
已知sin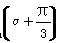 +sin α=-
+sin α=-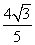 ,-
,-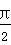 <α<0,则cos
<α<0,则cos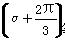 等于( )
等于( )
A.-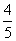 B.-
B.-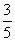
C.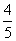 D.
D.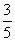
科目:高中数学 来源: 题型:
已知函数f(x)=|cos x|sin x,给出下列五个说法:
①f =-
=-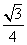 ;
;
②若|f(x1)|=|f(x2)|,则x1=x2+kπ(k∈Z);
③f(x)在区间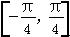 上单调递增;
上单调递增;
④函数f(x)的周期为π;
⑤f(x)的图象关于点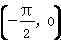 成中心对称.
成中心对称.
其中正确说法的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
在斜三角形ABC中,“A>B”是“|tan A|>|tan B|”的( )
A.充分必要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
在△ABC中,a,b,c是角A,B,C对应的边,向量m=(a+b,c),n=(a+b,-c),且m·n=( +2)ab.
+2)ab.
(1)求角C;
(2)函数f(x)=2sin(A+B)cos2(ωx)-cos(A+B)sin(2ωx)-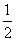 (ω>0)的相邻两个极值的横坐标分别为x0-
(ω>0)的相邻两个极值的横坐标分别为x0-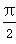 ,x0,求f(x)的单调递减区间.
,x0,求f(x)的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
设数列{an}满足a1=2,a2+a4=8,且对任意的n∈N*,都有an+an+2=2an+1.
(1)求数列{an}的通项公式;
(2)设数列{bn}的前n项和为Sn,且满足S1Sn=2bn-b1,n∈N*,b1≠0,求数列{anbn}的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com