
在△ABC中,a,b,c是角A,B,C对应的边,向量m=(a+b,c),n=(a+b,-c),且m·n=( +2)ab.
+2)ab.
(1)求角C;
(2)函数f(x)=2sin(A+B)cos2(ωx)-cos(A+B)sin(2ωx)-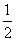 (ω>0)的相邻两个极值的横坐标分别为x0-
(ω>0)的相邻两个极值的横坐标分别为x0-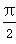 ,x0,求f(x)的单调递减区间.
,x0,求f(x)的单调递减区间.
科目:高中数学 来源: 题型:
若数列{an}的前n项和为Sn,有下列命题:
(1)若数列{an}是递增数列,则数列{Sn}也是递增数列;
(2)无穷数列{an}是递增数列,则至少存在一项ak,使得ak>0;
(3)若{an}是等差数列(公差d≠0),则S1·S2·…·Sk=0的充要条件是a1·a2·…·ak=0;
(4)若{an}是等比数列,则S1·S2·…·Sk=0(k≥2)的充要条件是an+an+1=0.
其中,正确命题的个数是( )
A.0 B.1
C.2 D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
各项均为正数的等比数列{an}满足a1a7=4,a6=8,若函数f(x)=a1x+a2x2+a3x3+…+a10x10的导数为f′(x),则f′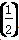 的值为________.
的值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)的定义域为R,则“f(x)在[-2,2]上单调递增”是“f(-2)<f(2)”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com