练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知a，b，c分别为△ABC三个内角A，B，C的对边，acos C＋asin C－b－c＝0，则A＝________.


    　

    [解析]　由题意，得

    sin Acos C＋sin Asin C＝sin B＋sin C，

    ∴sin Acos C＋sin Asin C＝sin(A＋C)＋sin C，

    ∴sin Acos C＋sin Asin C＝sin Acos C＋cos Asin C＋sin C.

    ∵sin C≠0，∴sin A－cos A＝1，

    即sin A－cos A＝，


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知平面向量若则实数         

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数h(x)＝2sin的图象与函数f(x)的图象关于点(0,1)对称，则函数f(x)可由h(x)经过________的变换得到．(　　)

    A．向上平移2个单位，向右平移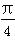个单位   

    B．向上平移2个单位，向左平移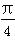个单位

    C．向下平移2个单位，向右平移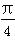个单位   

    D．向下平移2个单位，向左平移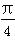个单位

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在斜三角形ABC中，“A>B”是“|tan A|>|tan B|”的(　　)

    A．充分必要条件                         B．充分不必要条件

    C．必要不充分条件                       D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图所示，某电力公司为保护一墙角处的电塔，计划利用墙OA，OB，再修建一长度为AB的围栏，围栏的造价与AB的长度成正比．现已知墙角∠AOB的度数为120°，当△AOB的面积为时，就可起到保护作用．则当围栏的造价最低时，∠ABO＝(　　)

    A．30°                                 B．45°

    C．60°                                 D．90°

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，a，b，c是角A，B，C对应的边，向量m＝(a＋b，c)，n＝(a＋b，－c)，且m·n＝(＋2)ab.

    (1)求角C；

    (2)函数f(x)＝2sin(A＋B)cos2(ωx)－cos(A＋B)sin(2ωx)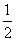－(ω>0)的相邻两个极值的横坐标分别为x0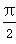－，x0，求f(x)的单调递减区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}满足an＝logn＋1(n＋2)(n∈N*)，定义使a1·a2·a3·…·ak为整数的数k(k∈N*)叫做幸运数，则k∈[1,2 014]内所有的幸运数的和为(　　)

    A．1 013                                B．1 560 

    C．2 026                                D．2 088

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    等比数列{an}满足an>0，n＝1,2，….且a5·a2n－5＝22n(n≥3)，则当n≥1时，log2a1＋log2a3＋…＋log2a2n－1＝(　　)

    A．(n－1)2                              B．(n＋1)2 

    C．n(2n－1)                             D．n2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列直线中，与直线x－2y+1=0垂直的是                                （　　）

    A.2x－y－3=0    B.x－2y+3=0         C.2x+y+5=0          D.x+2y－5=0

    查看答案和解析>>

    同步练习册答案