练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知数列{an}满足an＝logn＋1(n＋2)(n∈N*)，定义使a1·a2·a3·…·ak为整数的数k(k∈N*)叫做幸运数，则k∈[1,2 014]内所有的幸运数的和为(　　)

    A．1 013                                B．1 560 

    C．2 026                                D．2 088


    　C

    [解析]　由题可得a1·a2·a3·…·ak

    ＝log23·log34·log45·…·logk＋1(k＋2)

    ＝···…·

    ＝log2(k＋2)为整数，

    即log2(k＋2)＝m，m∈Z，则k＝2m－2，结合k∈[1,2014]，则k∈{2,6,14,30,62,126,254,510,1 022}，所以2＋6＋14＋30＋62＋126＋254＋510＋1 022＝(22＋23＋…＋210)－18＝2 026，故选C.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知函数，且，

    （1）求、的值；    （2）当时，求的最大值

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)＝＋2sin x.

    (1)在△ABC中，cos A＝－，求f(A)的值；

    (2)求函数f(x)的最小正周期及其图象的所有对称轴的方程．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a，b，c分别为△ABC三个内角A，B，C的对边，acos C＋asin C－b－c＝0，则A＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知等差数列{an}中，Sn为其前n项和，若a1＝－3，S5＝S10，则当Sn取到最小值时n的值为(　　)

    A．5                                    B．7 

    C．8                                    D．7或8

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若数列{an}的前n项和为Sn，有下列命题：

    (1)若数列{an}是递增数列，则数列{Sn}也是递增数列；

    (2)无穷数列{an}是递增数列，则至少存在一项ak，使得ak>0；

    (3)若{an}是等差数列(公差d≠0)，则S1·S2·…·Sk＝0的充要条件是a1·a2·…·ak＝0；

    (4)若{an}是等比数列，则S1·S2·…·Sk＝0(k≥2)的充要条件是an＋an＋1＝0.

    其中，正确命题的个数是(　　)

    A．0                                    B．1 

    C．2                                    D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}的前n项和为Sn，且a1＝0，对任意n∈N*，都有nan＋1＝Sn＋n(n＋1)．

    (1)求数列{an}的通项公式；

    (2)若数列{bn}满足an＋log2n＝log2bn，求数列{bn}的前n项和Tn.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，矩形AnBnCnDn的一边AnBn在x轴上，另外两个顶点Cn，Dn在函数f(x)＝x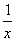＋(x>0)的图象上．若点Bn的坐标为(n,0)(n≥2，n∈N*)，记矩形AnBnCnDn的周长为an，则a2＋a3＋…＋a10＝(　　)

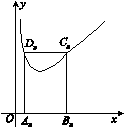
    A．208                                  B．216 

    C．212                                  D．220

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设某产品2013年12月底价格为a元（a>0），在2014年的前6个月，价格平均每月比上个月上涨10%，后6个月，价格平均每月比上个月下降10%，经过这12个月，2014年12月底该产品的价格为b元，则a，b的大小关系是                        （　　）

    A.a>b               B.a<b               C.a=b               D.不能确定

    查看答案和解析>>

    同步练习册答案