
已知数列{an}的前n项和为Sn,且a1=0,对任意n∈N*,都有nan+1=Sn+n(n+1).
(1)求数列{an}的通项公式;
(2)若数列{bn}满足an+log2n=log2bn,求数列{bn}的前n项和Tn.
解:(1)解法一:∵nan+1=Sn+n(n+1),
∴当n≥2时,(n-1)an=Sn-1+n(n-1),
两式相减,得nan+1-(n-1)an=Sn-Sn-1+n(n+1)-n(n-1),
即nan+1-(n-1)an=an+2n,化简,得an+1-an=2.
当n=1时,1×a2=S1+1×2,即a2-a1=2.
∴数列{an}是以0为首项,2为公差的等差数列.
∴an=2(n-1)=2n-2.
解法二:由nan+1=Sn+n(n+1),得
n(Sn+1-Sn)=Sn+n(n+1),
整理,得nSn+1=(n+1)Sn+n(n+1),
两边同除以n(n+1),得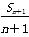 -
-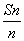 =1.
=1.
∴数列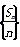 是以
是以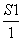 =0为首项,1为公差的等差数列.
=0为首项,1为公差的等差数列.
∴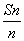 =0+n-1=n-1.
=0+n-1=n-1.
∴Sn=n(n-1).
当n≥2时,an=Sn-Sn-1=n(n-1)-(n-1)(n-2)=2n-2.
又a1=0适合上式,
∴数列{an}的通项公式为an=2n-2.
(2)∵an+log2n=log2bn,
∴bn=n·2an=n·22n-2=n·4n-1.
∴Tn=b1+b2+b3+…+bn-1+bn=40+2×41+3×42+…+(n-1)×4n-2+n×4n-1, ①
4Tn=41+2×42+3×43+…+(n-1)×4n-1+n×4n, ②
①-②,得-3Tn=40+41+42+…+4n-1-n·4n=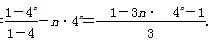
∴Tn=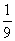 [(3n-1)·4n+1].
[(3n-1)·4n+1].


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:
水箱中有水20m3,如果打开出水孔,水箱中的水5min可以流完,当打开出水孔时,水箱中的水的剩余量V m3是时间t(s)的函数,则
m3是时间t(s)的函数,则 函数V=f(t)的解析式为_______
函数V=f(t)的解析式为_______
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,某电力公司为保护一墙角处的电塔,计划利用墙OA,OB,再修建一长度为AB的围栏,围栏的造价与AB的长度成正比.现已知墙角∠AOB的度数为120°,当△AOB的面积为 时,就可起到保护作用.则当围栏的造价最低时,∠ABO=( )
时,就可起到保护作用.则当围栏的造价最低时,∠ABO=( )
A.30° B.45°
C.60° D.90°
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}满足an=logn+1(n+2)(n∈N*),定义使a1·a2·a3·…·ak为整数的数k(k∈N*)叫做幸运数,则k∈[1,2 014]内所有的幸运数的和为( )
A.1 013 B.1 560
C.2 026 D.2 088
查看答案和解析>>
科目:高中数学 来源: 题型:
公比为q的等比数列{an}的前n项和为Sn,且a2+a4=20,a3+a5=40,设Tn=n(Sn+q),则数列{Tn}的前n项和为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
等比数列{an}满足an>0,n=1,2,….且a5·a2n-5=22n(n≥3),则当n≥1时,log2a1+log2a3+…+log2a2n-1=( )
A.(n-1)2 B.(n+1)2
C.n(2n-1) D.n2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com