
公比为q的等比数列{an}的前n项和为Sn,且a2+a4=20,a3+a5=40,设Tn=n(Sn+q),则数列{Tn}的前n项和为________.
 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:
已知数列{an}前n项和为Sn=1-5+9-13+17-21+…+(-1)n-1(4n-3),则S15+S22-S31的值是( )
A.13 B.-76
C.46 D.76
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}的前n项和为Sn,且a1=0,对任意n∈N*,都有nan+1=Sn+n(n+1).
(1)求数列{an}的通项公式;
(2)若数列{bn}满足an+log2n=log2bn,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
计算机是将信息转换成二进制进行处理的,二进制即“逢二进一”,如(1 101)2表示二进制数,将它转换成十进制数是1×23+1×22+0×21+1×20=13,那么将二进制数(11…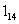 01)2转换成十进制数是( )
01)2转换成十进制数是( )
A.216-1 B.216-2
C.216-3 D.216-4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com