解:(Ⅰ)当n=1时,a
1=5a
1+1,∴
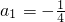
.又∵a
n=5S
n+1,a
n+1=5S
n+1+1
∴a
n+1-a
n=5a
n+1,即
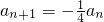
,∴数列{a
n}成等比数列,其首项
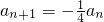
∴
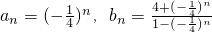
(II)证明:由(I)知由b
n=4+
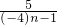
,∴b
2k-1+b
2k=8+
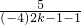

(-4)2k-1=8
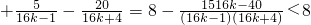
(Ⅲ)不存在正整数k,使得R
k≥4k成立.证明如下:
∴当n为偶数时,设n=2m(m∈N
*),∴R
n=(b
1+b
2)+(b
3+b
4)+…+(b
2m-1+b
2m)<8m=4n
当n为奇数时,设n=2m-1(m∈N
*),∴R
n=(b
1+b
2)+(b
3+b
4)+…+(b
2m-3+b
2m-2)+b
2m-1<8m-4=4n
∴对于一切的正整数n,都有R
n<4n,∴不存在正整数k,使得R
k≥4k成立.
分析:(Ⅰ)令n等于1代入a
n=5s
n+1中,即可求出首项a
1,然后把n换为n+1,利用a
n=5s
n+1表示出a
n+1,两个式子相减并利用S
n+1-S
n=a
n化简后即可得到

的值即为公比,得到此数列为等比数列,然后根据首项和公比写出数列的通项公式即可,因而可得出b
n的通项公式;
(Ⅱ)由(I)知由b
n=4+
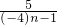
,从而可证;
(Ⅲ)根据b
n的通项公式,算出的前n项和为R
n,再计算出是否存在正整数k.
点评:此题考查学生灵活运用等比数列的通项公式及前n项和的公式化简求出,会确定一个数列为等比数列,考查数列递推式的求解及相关计算.是一道综合题.

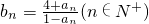 .,
.,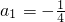 .又∵an=5Sn+1,an+1=5Sn+1+1
.又∵an=5Sn+1,an+1=5Sn+1+1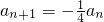 ,∴数列{an}成等比数列,其首项
,∴数列{an}成等比数列,其首项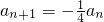
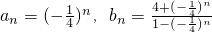
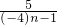 ,∴b2k-1+b2k=8+
,∴b2k-1+b2k=8+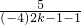
 (-4)2k-1=8
(-4)2k-1=8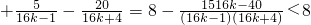
 的值即为公比,得到此数列为等比数列,然后根据首项和公比写出数列的通项公式即可,因而可得出bn的通项公式;
的值即为公比,得到此数列为等比数列,然后根据首项和公比写出数列的通项公式即可,因而可得出bn的通项公式;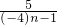 ,从而可证;
,从而可证;
