
甲、乙、丙三人进行乒乓球练习赛,其中两人比赛,另一人当裁判,每局比赛结束时,负的一方在下一局当裁判.设各局中双方获胜的概率均为 ,各局比赛的结果相互独立,第1局甲当裁判.
,各局比赛的结果相互独立,第1局甲当裁判.
(1)求第4局甲当裁判的概率;
(2)用X表示前4局中乙当裁判的次数,求X的分布列和数学期望.
(1)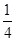 (2)
(2)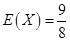
解析试题分析:(1)根据题意,甲第一局当裁判,则第二局一定是参加比赛,第四局当裁判,说明第三局继续参加比赛,所以,甲参加了第二、三两局的比赛,且第二局胜,第三局负.
科目:高中数学
来源:
题型:解答题
袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个,已知从袋子中随机抽取1个小球,取到标号为2的小球的概率是
科目:高中数学
来源:
题型:解答题
某校为组建校篮球队,对报名同学进行定点投篮测试,规定每位同学最多投3次,每次在A或B处投篮,在A处投进一球得3分,在B处投进一球得2分,否则得0分,每次投篮结果相互独立,将得分逐次累加并用X表示,如果X的值不低于3分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮方案有以下两种:
科目:高中数学
来源:
题型:解答题
为了参加2013年市级高中篮球比赛,该市的某区决定从四所高中学校选出
科目:高中数学
来源:
题型:解答题
小波以游戏方式决定:是去打球、唱歌还是去下棋.游戏规则为:以O为起点,再从A1,A2,A3,A4,A5,A6(如图)这6个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若
科目:高中数学
来源:
题型:解答题
袋内装有6个球,这些球依次被编号为1、2、3、……、6,设编号为n的球重n2-6n+12(单位:克),这些球等可能地从袋里取出(不受重量、编号的影响).
科目:高中数学
来源:
题型:解答题
学校游园活动有这样一个游戏项目:甲箱子里装有3个白球,2个黑球,乙箱子里装有1个白球,2个黑球,这些球除颜色外完全相同.每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖(每次游戏结束后将球放回原箱).
科目:高中数学
来源:
题型:解答题
以下茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以X表示.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
(2)根据题意,在四局比赛中,乙参赛的情况与比赛结果可用下表表示五种情况: 第一局 第二局 第三局 第四局 当裁判次数 1 参赛(胜) 参赛(胜) 参赛(胜) 参赛 0 2 参赛(胜) 参赛(胜) 参赛(负) 裁判 1 3 参赛(胜) 参赛(负) 裁判 参赛 1 4 参赛(负) 裁判 参赛(胜) 参赛 1 5 

西城学科专项测试系列答案
小考必做系列答案
小考实战系列答案
小考复习精要系列答案
小考总动员系列答案
小升初必备冲刺48天系列答案
68所名校图书小升初高分夺冠真卷系列答案
伴你成长周周练月月测系列答案
小升初金卷导练系列答案
萌齐小升初强化模拟训练系列答案
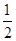 .
.
(1)求n的值;
(2)从袋子中不放回地随机抽取2个球,记第一次取出小球标号为a,第二次取出的小球标号为b.①记“a+b=2”为事件A,求事件A的概率;
②在区间[0,2]内任取2个实数x,y,求事件“x2+y2>(a-b)2恒成立”的概率.
方案1:先在A处投一球,以后都在B处投;
方案2:都在B处投篮.
已知甲同学在A处投篮的命中率为0.4,在B处投篮的命中率为0.6.
(1)甲同学若选择方案1,求X=2时的概率;
(2)甲同学若选择方案2,求X的分布列和数学期望;
(3)甲同学选择哪种方案通过测试的可能性更大?请说明理由. 人组成男子篮球队代表所在区参赛,队员来源人数如下表:
人组成男子篮球队代表所在区参赛,队员来源人数如下表:
该区篮球队经过奋力拼搏获得冠军,现要从中选出两名队员代表冠军队发言.学校
学校甲
学校乙
学校丙
学校丁
人数
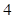
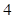
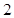
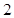
(Ⅰ)求这两名队员来自同一学校的概率;
(Ⅱ)设选出的两名队员中来自学校甲的人数为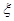 ,求随机变量
,求随机变量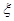 的分布列及数学期望
的分布列及数学期望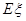 .
.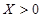 就去打球;若
就去打球;若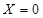 就去唱歌;若
就去唱歌;若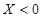 就去下棋.
就去下棋.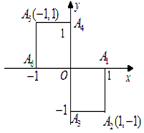
(Ⅰ)分别求小波去下棋的概率和不去唱歌的概率.
(Ⅱ)写出数量积X的所有可能取值,并求X分布列与数学期望
(1)从袋中任意取出一个球,求其重量大于其编号的概率;
(2)如果不放回地任意取出2个球,求它们重量相等的概率.
(1)求在1次游戏中:
①摸出3个白球的概率;②获奖的概率.
(2)求在两次游戏中获奖次数X的分布列及数学期望E(X).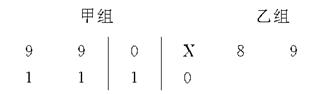
(1)如果X=8,求乙组同学植树棵数的平均数和方差;
(2)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数Y的分布列和数学期望.(注:方差s2=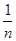 [(x1-
[(x1- )2+(x2-
)2+(x2- )2+…+(xn-
)2+…+(xn- )2],其中
)2],其中 为x1,x2,…,xn的平均数)
为x1,x2,…,xn的平均数)
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号