
【题目】对两个变量y和x进行回归分析,得到一组样本数据:(x1 , y1),(x2 , y2),…,(xn , yn),则下列说法中不正确的是( )
A.由样本数据得到的回归方程 ![]() =
= ![]() x+
x+ ![]() 必过样本中心(
必过样本中心( ![]() ,
, ![]() )
)
B.残差平方和越小的模型,拟合的效果越好
C.用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好
D.两个随机变量的线性相关性越强,相关系数的绝对值越接近于1
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1).当![]() 时,求
时,求![]() 的单调增区间;
的单调增区间;
(2)当![]() ,对于任意
,对于任意![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 的图象始终在直线
的图象始终在直线![]() 的下方,求实数
的下方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x+1)ln x-a(x-1).
(1)当a=4时,求曲线y=f(x)在(1,f(1))处的切线方程;
(2)若当x∈(1,+∞)时,f(x)>0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):
规定若满意度不低于98分,测评价该教师为“优秀”.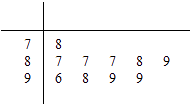
(1)求从这10人中随机选取3人,至多有1人评价该教师是“优秀”的概率;
记ξ表示抽到评价该教师为“优秀”的人数,求ξ的分布列及数学期望.
(2)以这10人的样本数据来估计整个班级的总体数据,若从该班任选3人,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的极坐标方程为ρ=2cosθ,直线l的参数方程为 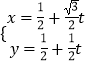 (t为参数),点A的极坐标为(
(t为参数),点A的极坐标为( ![]() ,
, ![]() ),设直线l与圆C交于点P、Q.
),设直线l与圆C交于点P、Q.
(1)写出圆C的直角坐标方程;
(2)求|AP||AQ|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com