
分析 由分段函数解析式结合f[f(-$\frac{1}{2}$)]=$\frac{1}{2}$求得a值;求出分段函数的值域,由并集为R求得a的范围.
解答 解:∵f(x)=$\left\{\begin{array}{l}x+1,x≤0\\ x+\frac{4}{x}-a,x>0\end{array}$,
∴f(-$\frac{1}{2}$)=$-\frac{1}{2}+1=\frac{1}{2}$,则f[f(-$\frac{1}{2}$)]=f($\frac{1}{2}$)=$\frac{1}{2}$+$\frac{4}{\frac{1}{2}}-a$=$\frac{1}{2}$+8-a=$\frac{1}{2}$,得a=8;
由y=x+1,x≤0,得y≤1;
由y=$x+\frac{4}{x}-a$,x>0,得y≥4-a,
∵f(x)的值域为R,∴4-a≤1,得a≥3.
故答案为:8;a≥3.
点评 本题考查简单的线性规划,考查了分段函数的应用,是中档题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
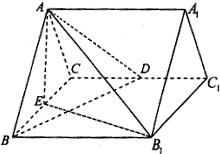 如图,已知正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点,E为BC的中点.
如图,已知正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点,E为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
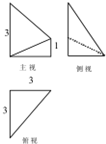
| A. | 18cm3 | B. | 6cm3 | C. | $\frac{9}{2}c{m^3}$ | D. | $\frac{27}{2}c{m^3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD=1,EC⊥BD,∠BCD=120°,EA=2,M是EC上的点,且EM=3MC.
如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD=1,EC⊥BD,∠BCD=120°,EA=2,M是EC上的点,且EM=3MC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
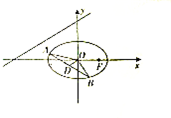 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,右焦点F到直线x=$\frac{a^2}{c}$的距离为1.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,右焦点F到直线x=$\frac{a^2}{c}$的距离为1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1) | B. | $[0,2)∪\{-\frac{18}{e^2}\}$ | C. | $(0,2)∪\{-\frac{18}{e^2}\}$ | D. | $[0,2\sqrt{e})∪\{-\frac{18}{e^2}\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com