


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
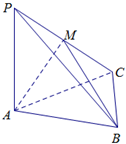 如图,底面是正三角形的三棱锥P-ABC中,PA⊥底面ABC,M为PC中点,且PA=AB,其中下列四个命题:
如图,底面是正三角形的三棱锥P-ABC中,PA⊥底面ABC,M为PC中点,且PA=AB,其中下列四个命题:| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 所持态度 | 喜欢方案A | 喜欢方案B | 喜欢方案C | 三种方案都不喜欢 |
| 人数(单位:人) | 25 | 50 | 100 | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
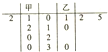 2014年1月8日是传统的腊八节,大家开始购买年货,某淘宝网店趁势推出“抢红包”的促销活动,已知每人有5次抢红包的机会,每次可得1至30元不等的红包,甲、乙二人在这5次抢红包活动中获得红包金额的茎叶图如图所示,若甲5次获得红包金额的均值为
2014年1月8日是传统的腊八节,大家开始购买年货,某淘宝网店趁势推出“抢红包”的促销活动,已知每人有5次抢红包的机会,每次可得1至30元不等的红包,甲、乙二人在这5次抢红包活动中获得红包金额的茎叶图如图所示,若甲5次获得红包金额的均值为. |
| x1 |
| x2 |
. |
| x1 |
. |
| x2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com