
【题目】已知一个口袋有m个白球,n个黑球(m,n![]()
![]() ,n
,n![]() 2),这些球除颜色外全部相同。现将口袋中的球随机的逐个取出,并放入如图所示的编号为1,2,3,……,m+n的抽屉内,其中第k次取球放入编号为k的抽屉(k=1,2,3,……,m+n).
2),这些球除颜色外全部相同。现将口袋中的球随机的逐个取出,并放入如图所示的编号为1,2,3,……,m+n的抽屉内,其中第k次取球放入编号为k的抽屉(k=1,2,3,……,m+n).
![]()
(1)试求编号为2的抽屉内放的是黑球的概率p;
(2)随机变量x表示最后一个取出的黑球所在抽屉编号的倒数,E(x)是x的数学期望,证明 ![]()
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:(1)根据条件先确定总事件数为![]() ,而编号为2的抽屉内放的是黑球的事件数为
,而编号为2的抽屉内放的是黑球的事件数为![]() ,最后根据古典概型的概率公式即可求概率;(2)先确定最后一个取出的黑球所在抽屉编号的倒数为
,最后根据古典概型的概率公式即可求概率;(2)先确定最后一个取出的黑球所在抽屉编号的倒数为![]() ,所对应的概率
,所对应的概率![]() ,再根据数学期望公式得
,再根据数学期望公式得![]() ,利用性质
,利用性质![]() ,进行放缩变形:
,进行放缩变形: ![]() ,最后利用组合数性质
,最后利用组合数性质![]() 化简,可得结论.
化简,可得结论.
试题解析:解:(1)编号为2的抽屉内放的是黑球的概率![]() 为:
为: ![]() .
.
(2)随机变量X的概率分布为:
X |
|
|
| … |
| … |
|
P |
|
|
| … |
| … |
|
随机变量X的期望为:
![]() .
.
所以![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
点睛:求解离散型随机变量的数学期望的一般步骤为:
(1)“判断取值”,即判断随机变量的所有可能取值,以及取每个值所表示的意义;
(2)“探求概率”,即利用排列组合、枚举法、概率公式(常见的有古典概型公式、几何概型公式、互斥事件的概率和公式、独立事件的概率积公式,以及对立事件的概率公式等),求出随机变量取每个值时的概率;
(3)“写分布列”,即按规范形式写出分布列,并注意用分布列的性质检验所求的分布列或某事件的概率是否正确;
(4)“求期望值”,一般利用离散型随机变量的数学期望的定义求期望的值,对于有些实际问题中的随机变量,如果能够断定它服从某常见的典型分布(如二项分布![]() ),则此随机变量的期望可直接利用这种典型分布的期望公式(
),则此随机变量的期望可直接利用这种典型分布的期望公式(![]() )求得.因此,应熟记常见的典型分布的期望公式,可加快解题速度.
)求得.因此,应熟记常见的典型分布的期望公式,可加快解题速度.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:
【题目】从某大学一年级女生中,选取身高分别是150cm、155cm、160cm、165cm、170cm的学生各一名,其身高和体重数据如表所示:
身高/cm(x) | 150 | 155 | 160 | 165 | 170 |
体重/kg(y) | 43 | 46 | 49 | 51 | 56 |
(1)求y关于x的线性回归方程;
(2)利用(1)中的回归方程,计算身高为168cm时,体重的估计值 ![]() 为多少?
为多少?
参考公式:线性回归方程 ![]() =
= ![]() x+
x+ ![]() ,其中
,其中 ![]() =
=  =
= 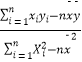 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正三棱锥P﹣ABC底面边长为6,底边BC在平面α内,绕BC旋转该三棱锥,若某个时刻它在平面α上的正投影是等腰直角三角形,则此三棱锥高的取值范围是( ) 
A.(0, ![]() ]
]
B.(0, ![]() ]∪[
]∪[ ![]() ,3]
,3]
C.(0, ![]() ]
]
D.(0, ![]() ]∪[3,
]∪[3, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—5:不等式选讲]
已知函数f(x)=–x2+ax+4,g(x)=│x+1│+│x–1│.
(1)当a=1时,求不等式f(x)≥g(x)的解集;
(2)若不等式f(x)≥g(x)的解集包含[–1,1],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,BC=2,原点O是BC的中点,点A的坐标为 ( ![]() ,0),点D在平面yOz上,且∠BDC=90°,∠DCB=30°.
,0),点D在平面yOz上,且∠BDC=90°,∠DCB=30°. 
(1)求向量 ![]() 的坐标
的坐标
(2)求向量 ![]() 的夹角的余弦值大小.
的夹角的余弦值大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,平面四边形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AD⊥ED,AF∥DE,AB∥CD,CD=2AB=2AD=2ED=xAF.
(Ⅰ)若四点F、B、C、E共面,AB=a,求x的值;
(Ⅱ)求证:平面CBE⊥平面EDB;
(Ⅲ)当x=2时,求二面角F﹣EB﹣C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数  ,设F(x)=x2f(x),则F(x)是( )
,设F(x)=x2f(x),则F(x)是( )
A.奇函数,在(﹣∞,+∞)上单调递减
B.奇函数,在(﹣∞,+∞)上单调递增
C.偶函数,在(﹣∞,0)上递减,在(0,+∞)上递增
D.偶函数,在(﹣∞,0)上递增,在(0,+∞)上递减
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100 个网箱,测量各箱水产品的产量(单位:kg).其频率分布直方图如下:

(1)设两种养殖方法的箱产量相互独立,记A表示事件:“旧养殖法的箱产量低于50kg,新养殖法的箱产量不低于50kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50kg | 箱产量≥50kg | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,求新养殖法箱产量的中位数的估计值(精确到0.01).
附: ,
, 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com