
【题目】若函数![]() 的导函数
的导函数![]() ,
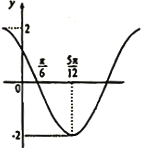
,![]() 的部分图象如图所示,
的部分图象如图所示,![]() ,当
,当![]() ,
,![]() 时,则
时,则![]() 的最大值为_________.
的最大值为_________.
【答案】![]()
【解析】
由图象可得:A=2,![]() ,解得ω=2.可得f′(x)=2cos(2
,解得ω=2.可得f′(x)=2cos(2![]() φ)=﹣2,|φ|
φ)=﹣2,|φ|![]() ),把x
),把x![]() ,
,![]() 2代入解得φ.可得f′(x),进而得出f(x),g(x)=f(x
2代入解得φ.可得f′(x),进而得出f(x),g(x)=f(x![]() ),利用正弦函数的单调性即可得出结论.
),利用正弦函数的单调性即可得出结论.
由图象可得:A=2,![]() ,解得ω=2.
,解得ω=2.
∴f′(x)=2cos(2![]() φ)=﹣2,|φ|
φ)=﹣2,|φ|![]() ),解得φ
),解得φ![]() .
.
∴f′(x)=2cos(2x![]() ).
).
∴f(x)=sin(2x![]() )+c.(c为常数).
)+c.(c为常数).
g(x)=f(x![]() )=sin2x+c.
)=sin2x+c.
x∈[![]() ,
,![]() ]时,2x∈
]时,2x∈![]() .
.
sin2x∈![]() ,
,
当x1,x2∈[![]() ,
,![]() ]时,则|g(x1)﹣g(x2)|=|sin2x1﹣sin2x2|≤1﹣(
]时,则|g(x1)﹣g(x2)|=|sin2x1﹣sin2x2|≤1﹣(![]() )
)![]() .
.
因此当x1,x2∈[![]() ,
,![]() ]时,则|g(x1)﹣g(x2)|的最大值为
]时,则|g(x1)﹣g(x2)|的最大值为![]() .
.
故答案为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,写出
,写出![]() 所有可能的值;
所有可能的值;
(2)若数列![]() 是递增数列,且
是递增数列,且![]() 、
、![]() 、
、![]() 成等差数列,求p的值;
成等差数列,求p的值;
(3)若![]() ,且
,且![]() 是递增数列,
是递增数列,![]() 是递减数列,求数列
是递减数列,求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
: ![]() 的长轴长为4,离心率为
的长轴长为4,离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过右焦点![]() 作一条不与坐标轴平行的直线
作一条不与坐标轴平行的直线![]() ,若
,若![]() 交椭圆
交椭圆![]() 与
与![]() 、
、![]() 两点,点
两点,点![]() 关于原点
关于原点![]() 的对称点为
的对称点为![]() ,求
,求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中:
①已知函数![]() 的定义域为
的定义域为![]() ,则函数
,则函数![]() 的定义域为
的定义域为![]() ;
;
②若集合![]() 中只有一个元素,则
中只有一个元素,则![]() ;
;
③函数![]() 在
在![]() 上是增函数;
上是增函数;
④方程![]() 的实根的个数是1.
的实根的个数是1.
所有正确命题的序号是______(请将所有正确命题的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解学生假期参与志愿服务活动的情况,随机调查了![]() 名男生,
名男生,![]() 名女生,得到他们一周参与志愿服务活动时间的统计数据如右表(单位:人):
名女生,得到他们一周参与志愿服务活动时间的统计数据如右表(单位:人):
超过 | 不超过 | |
男 |
|
|
女 |
|
|
(1)能否有![]() 的把握认为该校学生一周参与志愿服务活动时间是否超过
的把握认为该校学生一周参与志愿服务活动时间是否超过![]() 小时与性别有关?
小时与性别有关?
(2)以这![]() 名学生参与志愿服务活动时间超过
名学生参与志愿服务活动时间超过![]() 小时的频率作为该事件发生的概率,现从该校学生中随机抽查
小时的频率作为该事件发生的概率,现从该校学生中随机抽查![]() 名学生,试估计这
名学生,试估计这![]() 名学生中一周参与志愿服务活动时间超过
名学生中一周参与志愿服务活动时间超过![]() 小时的人数.
小时的人数.
附:
|
|
|
|
|
|
|
|
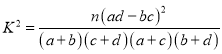
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工程队共有500人,要建造一段6000米的高速公路,工程需要把500人分成两组,甲组的任务是完成一段4000米的软土地带,乙组的任务是完成剩下的2000米的硬土地带,据测算,软、硬土地每米的工程量是30工(工为计量单位)和40工.
(1)若平均分配两组的人数,分别计算两组完工的时间,并求出此时全队的筑路工期;
(2)如何分配两组的人数会使得全队的筑路工期最短?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次高三年级模拟考试中,数学试卷有一道满分10分的选做题,学生可以从A,B两道题目中任选一题作答.某校有900名高三学生参加了本次考试,为了了解该校学生解答该选做题的得分情况,作为下一步教学的参考依据,计划从900名考生的选做题成绩中随机抽取一个容量为10的样本,为此将900名考生选做题的成绩按照随机顺序依次编号为001~900.
(1)若采用系统抽样法抽样,从编号为001~090的成绩中用简单随机抽样确定的成绩编号为025,求样本中所有成绩编号之和;
(2)若采用分层抽样,按照学生选择A题目或B题目,将成绩分为两层.已知该校高三学生有540人选做A题目,有360人选做B题目,选取的样本中,A题目的成绩平均数为5,方差为2,B题目的成绩平均数为5.5,方差为0.25.
(i)用样本估计该校这900名考生选做题得分的平均数与方差;
(ii)本选做题阅卷分值都为整数,且选取的样本中,A题目成绩的中位数和B题目成绩的中位数都是5.5.从样本中随机选取两个大于样本平均值的数据做进一步调查,求取到的两个成绩来自不同题目的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com