分析:由线段A1M所在平面AD1A1与B1C所在平面BCC1B1互相平行,且直线A1M与B1C不平行,知线段A1M与B1C所在直线为异面直线;设正方体ABCD-A1B1C1D1的棱长为2,以DA为x轴,以DC为y轴,以DD1为z轴,建立空间直角坐标系,利用向量法能够得到对角线BD1⊥平面AB1C,平面AMC⊥平面AB1C,直线A1M与平面AB1C不平行.
解答:
解:∵线段A
1M所在平面AD
1A
1与B
1C所在平面BCC
1B
1互相平行,
且直线A
1M与B
1C不平行,
∴线段A
1M与B
1C所在直线为异面直线,
故①正确;
设正方体ABCD-A
1B
1C
1D
1的棱长为2,以DA为x轴,以DC为y轴,以DD
1为z轴,建立空间直角坐标系,
则A(2,0,0),B(2,2,0),C(0,2,0),B
1(2,2,2),M(0,0,1),D
1(0,0,2),
∴
=(0,2,2),
=(-2,2,0),
=(-2,-2,2),
=(-2,0,1),
∴
•=0-4+4=0,
•=4-4+0=0,
∴
⊥,
⊥,
∴BD
1⊥AB
1,BD
1⊥AC,
∴对角线BD
1⊥平面AB
1C,
故②正确;
设平面AMC的法向量为
=(x
1,y
1,z
1),则
•=0,
•=0,
∴
,∴
=(1,1,2),
设平面AB
1C的法向量为
=(x
2,y
2,z
2),则
•=0,
•=0,
∴
,∴
=(1,1,-1),
∵
•=1+1-2=0,
∴平面AMC⊥平面AB
1C,
故③正确;
∵A
1(2,0,2),M(0,0,1),
∴
=(-2,0,-1),
∵
•=-2+0+1=-1≠0,
∴直线A
1M与平面AB
1C不平行,
故④不正确.
故答案为:①②③.
点评:本题考查异面直线的判断,直线与平面垂直、平面与平面垂直、直线与平面平行的判断,解题时要认真审题,仔细解答,注意向量法的合理运用.

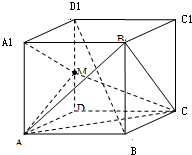 如图,在正方体ABCD-A1B1C1D1中,M是DD1的中点,则下列结论正确的是
如图,在正方体ABCD-A1B1C1D1中,M是DD1的中点,则下列结论正确的是 解:∵线段A1M所在平面AD1A1与B1C所在平面BCC1B1互相平行,
解:∵线段A1M所在平面AD1A1与B1C所在平面BCC1B1互相平行,

 阅读快车系列答案
阅读快车系列答案 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则