
设函数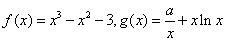 ,其中
,其中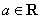 .
.
(1)若存在 ,使得
,使得 ,求整数
,求整数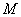 的最大值;
的最大值;
(2)若对任意的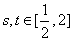 ,都有
,都有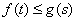 ,求
,求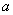 的取值范围.
的取值范围.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
下表中的数阵为“森德拉姆数筛”,其特点是每行每列都成等差数列,记第i行第j列的数为aij,则数字73在表中出现的次数为 _________ .
| 2 | 3 | 4 | 5 | 6 | 7 | … |
| 3 | 5 | 7 | 9 | 11 | 13 | … |
| 4 | 7 | 10 | 13 | 16 | 19 | … |
| 5 | 9 | 13 | 17 | 21 | 25 | … |
| 6 | 11 | 16 | 21 | 26 | 31 | … |
| 7 | 13 | 19 | 25 | 31 | 37 | … |
| … | … | … | … | … | … | … |
查看答案和解析>>
科目:高中数学 来源: 题型:
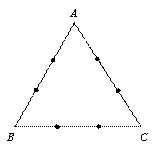
如图所示,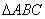 是边长为3的正三角形,若在每一边的两个三等分点中,各随机选取一点连成三角形,下列命题正确的是(写出所有正确命题的编号):
是边长为3的正三角形,若在每一边的两个三等分点中,各随机选取一点连成三角形,下列命题正确的是(写出所有正确命题的编号):
①依此方法可能连成的三角形一共有8个;
②这些可能连成的三角形中,恰有3个是直角三角形;
③这些可能连成的三角形中,恰有2个是锐角三角形;
④这些可能连成的三角形中,恰有2个是钝角三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
将1,2,3,4,5,6,7,8,9这9个正整数分别写在三张卡片上,要求每一张卡片上的三个数中任意两数之差都不在这张卡片上,现在第一张卡片上已经写有1和5,第二张卡片上写有2,第三张卡片上写有3,则第一张卡片上的另一个数字是 _________ .
查看答案和解析>>
科目:高中数学 来源: 题型:
将正偶数按下表排成4列:
第1列 第2列 第3列 第4列
第1行 2 4 6 8
第2行 16 14 12 10
第3行 18 20 22 24
… … 28 26
则2 004在 ( )
(A)第251行,第1列 (B)第251行,第2列
(C)第250行,第2列 (D)第250行,第4列
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com