
函数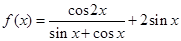 .
.
(Ⅰ)在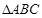 中,
中,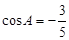 ,求
,求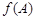 的值;
的值;
(Ⅱ)求函数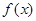 的最小正周期及其图象的所有对称轴的方程.
的最小正周期及其图象的所有对称轴的方程.
(Ⅰ)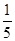 ;(Ⅱ)
;(Ⅱ)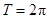 ,
,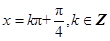
解析试题分析:(Ⅰ)由已知条件可求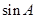 的值。化简函数
的值。化简函数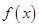 时余弦的二倍角公式有三个,分析可知应用
时余弦的二倍角公式有三个,分析可知应用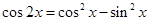 ,然后按平方差公式展开可消去分母将其化简,将
,然后按平方差公式展开可消去分母将其化简,将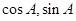 代入化简后的
代入化简后的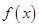 即可求
即可求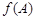 的值;(Ⅱ)用化一公式再将其继续化简为
的值;(Ⅱ)用化一公式再将其继续化简为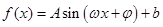 的形式。根据周期公式
的形式。根据周期公式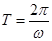 求周期,再将
求周期,再将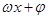 视为整体代入正弦函数对称轴公式
视为整体代入正弦函数对称轴公式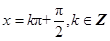 即可得其对称轴方程。
即可得其对称轴方程。
试题解析:解:(Ⅰ)由 得
得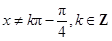 .
.
因为,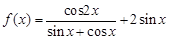
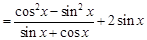 2分
2分
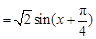 , 4分
, 4分
因为在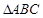 中,
中,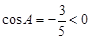 ,
,
所以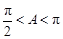 , 5分
, 5分
所以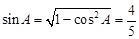 , 7分
, 7分
所以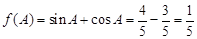 . 8分
. 8分
(Ⅱ)由(Ⅰ)可得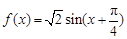 ,
,
所以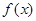 的最小正周期
的最小正周期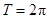 . 10分
. 10分
因为函数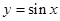 的对称轴为
的对称轴为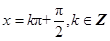 , 11分
, 11分
又由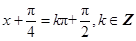 ,得
,得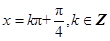 ,
,
所以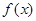 的对称轴的方程为
的对称轴的方程为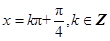 . 13分
. 13分
考点:用二倍角公式、化一公式等化简三角函数,正弦函数的周期及对称轴,考查整体思想及计算能力。


科目:高中数学 来源: 题型:解答题
已知x∈R,ω>0,u=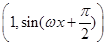 ,v=(cos2ωx,
,v=(cos2ωx,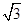 sin ωx),函数f(x)=u·v-
sin ωx),函数f(x)=u·v-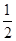 的最小正周期为π.
的最小正周期为π.
(1)求ω的值;
(2)求函数f(x)在区间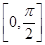 上的值域.
上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 .
.
(Ⅰ)请用“五点法”画出函数 在长度为一个周期的闭区间上的简图(先在所给的表格中填上所需的数值,再画图);
在长度为一个周期的闭区间上的简图(先在所给的表格中填上所需的数值,再画图);

(Ⅱ)求函数 的单调递增区间;
的单调递增区间;
(Ⅲ)当 时,求函数
时,求函数 的最大值和最小值及相应的
的最大值和最小值及相应的 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com