练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知点A(2,0),B(0,2),点C(x,y)在以原点为圆心的单位圆上.

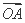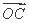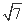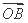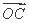    (1) 若|+|=(O为坐标原点),求向量与的夹角θ;

    (2) 若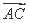⊥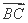,求点C的坐标.


     (1) 由=(2,0),=(x,y),得+=(2+x,y).

    由|+|=,得(2+x)2+y2=7,

    所以解得x=,y=±.

    cos θ===y=±,

    所以与的夹角为30°或150°.

    (2) =(x-2,y),=(x,y-2),由⊥,得·=0,则x2-2x+y2-2y=0.

    由

    解得或

    所以点C的坐标为

    或.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知函数f(x)=(2x-x2)·ex,给出以下四个判断:

    ①f(x)>0的解集是{x|0<x<2};②f(-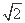)是极小值,f(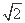)是极大值;③f(x)没有最小值,但有最大值;④f(x)既没有最大值,也没有最小值.其中判断正确的有　　　　.(填序号)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    定义函数φ(x)=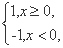f(x)=x2-2x(x2-a)φ(x2-a).

    (1) 解关于a的不等式f(1)≤f(0);

    (2) 已知函数f(x)在x∈[0,1]的最小值为f(1),求正实数a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     设数列{an}的前n项和为Sn,a1=3,且an+1=2Sn+3,数列{bn}为等差数列,且公差d>0,b1+b2+b3=15.

    (1) 求数列{an}的通项公式;

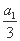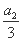    (2) 若+b1,+b2,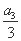+b3成等比数列,求数列{bn}的前n项和Tn.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图,在△ABC中,已知AB=2,BC=3,∠ABC=60°,AH⊥BC于点H,M为AH的中点,若=λ+μ,则λ+μ=　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若从1,2,3,…,9这9个整数中同时取4个不同的数,使其和为奇数,则不同的取法共有　　　　种.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设m,n∈N*,f(x)=(1+x)m+(1+x)n.

    (1) 当m=n=7时,f(x)=a7x7+a6x6+…+a1x+a0,求a0+a2+a4+a6的值;

    (2) 当m=n时,f(x)展开式中x2的系数是20,求n的值;

    (3) 若f(x)展开式中x的系数是19,当m,n变化时,求x2系数的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     如图,已知正三棱柱ABCA1B1C1的底面边长为2 cm,高为5 cm,一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为　　　　cm. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     中心在原点、焦点在x轴上的椭圆C的焦距为2,两准线间的距离为10.设点A(5,0),过点A作直线l交椭圆C于P,Q两点,过点P作x轴的垂线交椭圆C于另一点S.

    (1) 求椭圆C的方程;

    (2) 求证:直线SQ过x轴上一定点B;

    (3) 若过点A作直线与椭圆C只有一个公共点D,求过B,D两点、且以AD为切线的圆的方程.

    查看答案和解析>>

    同步练习册答案