练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若从1,2,3,…,9这9个整数中同时取4个不同的数,使其和为奇数,则不同的取法共有　　　　种.


    60　


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设直线y=x+b是曲线y=ln x(x>0)的一条切线,则实数b=　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设10件同类型的零件中有2件不合格品,从所有零件中依次不放回地取出3件,以X表示取出的3件中不合格品的件数.

    (1) 求“第一次取得正品且第二次取得次品”的概率;

    (2) 求X的概率分布和数学期望E(X).

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若|a|=3,|b|=4,(a+b)·(a+3b)=33,则a与b的夹角为　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知点A(2,0),B(0,2),点C(x,y)在以原点为圆心的单位圆上.

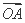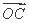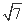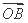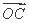    (1) 若|+|=(O为坐标原点),求向量与的夹角θ;

    (2) 若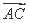⊥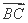,求点C的坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    7个人排成一排,在下列情况下,各有多少种不同排法

    (1) 甲不在排头,也不在排尾;

    (2) 甲、乙之间有且只有2人;

    (3) 甲、乙、丙3人两两相邻;

    (4)甲在乙的左边(不一定相邻).

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以AC为直径的圆交AB于点D,求BD,CD的长.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


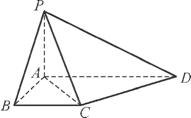
    如图,在四棱锥PABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,PA=AB=BC=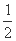AD.

    (1) 求证:CD⊥平面PAC;

    (2) 侧棱PA上是否存在点E,使得BE∥平面PCD?若存在,指出点E的位置并证明;若不存在,请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    当x2-2x<8时,函数y=的最小值为　　　　. 

    查看答案和解析>>

    同步练习册答案