
求函数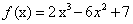 的单调区间和极值.
的单调区间和极值.
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
下列结论中正确的是 ( )
A. 导数为零的点一定是极值点
B. 如果在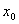 附近的左侧
附近的左侧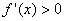 右侧
右侧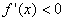 那么
那么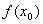 是极大值
是极大值
C. 如果在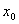 附近的左侧
附近的左侧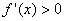 右侧
右侧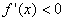 那么
那么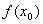 是极小值
是极小值
D. 如果在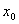 附近的左侧
附近的左侧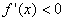 右侧
右侧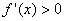 那么
那么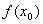 是极大值
是极大值
查看答案和解析>>
科目:高中数学 来源: 题型:
已知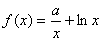 ,
, 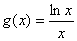 ,
,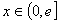 ,其中e是无理数且e=2.71828…,
,其中e是无理数且e=2.71828…,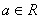 .
.
(1)若a=1,求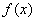 的单调区间与极值;
的单调区间与极值;
(2)求证:在(1)的条件下,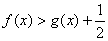 ;
;
(3)是否存在实数a,使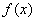 的最小值是-1?若存在,求出a的值;若不存在,说明理由.
的最小值是-1?若存在,求出a的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
某公司将4名新招聘的员工分配至3个不同的部门,每个部门至少分配一名员工.其中甲、乙两名员工必须在同一个部门的不同分配方法的总数为( )
A.6 B.12 C.24 D.36
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com