练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    函数在区间上的零点的个数为                        (   )

       A．2                 B．3                C．4                D．5


    C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    求函数的单调区间和极值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    16．(本小题满分13分)

    某渔池年初放养一批鱼苗，为了解这批鱼苗的生长、健康状况，一个月后，从该渔池中随机捞出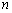条鱼称其重量（单位:克），并将所得数据进行分组，得到如右频率分布表．

    （Ⅰ）求频率分布表中的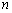，，的值；

    （Ⅱ）从捞出的重量不超过克的鱼中，随机抽取条作病理检测，记这条鱼中，重量不超过克的鱼的条数为，求的分布列和数学期望．

    分组

    频数

    频率

    (80，90]

    3

    0.03

    (90，100]

    7

    0.07

    (100，110]

    0.10

    (110，120]

    20

    (120，130]

    35

    0.35

    (130，140]

    20

    0.20

    (140，150]

    5

    0.05

    合计

    1.00

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若，则最大值为         ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    预计某地区明年从年初开始的前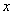个月内，对某种商品的需求总量 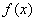（万件）近似满足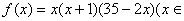：N*，且）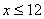

    （1）写出明年第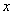个月的需求量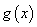（万件）与月份 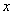的函数关系式，并求出哪个月份的需求量超过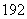万件；

    （2）如果将该商品每月都投放到该地区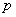万件（不包含积压商品），要保证每月都满足供应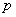， 应至少为多少万件？（积压商品转入下月继续销售）

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    不等式对任意，恒成立，则实数的取值范围是

    A．   B．       C．      D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设抛物线的焦点为，点，线段的中点在抛物线上. 设动直线与抛物线相切于点，且与抛物线的准线相交于点，以为直径的圆记为圆．

    （1）求的值；

    （2）证明：圆与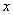轴必有公共点；

    （3）在坐标平面上是否存在定点，使得圆恒过点？若存在，求出的坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知是第四象限角,tan(则sin等于  (    )

    A.                                                                               B.   C.     D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    直线L：与椭圆C：交于A、B两点，以OA、OB为邻边作平行四边形OAPB。

    求证：椭圆C：与直线L：总有两个交点。当时，求点P的轨迹方程。

    （3）是否存在直线L，使OAPB为矩形？若存在，求出此时直线L的方程；若不存在，说明理由。

    查看答案和解析>>

    同步练习册答案