
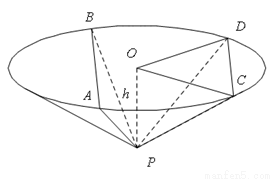
如图,圆锥顶点为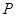 .底面圆心为
.底面圆心为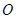 ,其母线与底面所成的角为
,其母线与底面所成的角为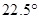 .
.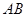 和
和 是底面圆
是底面圆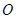 上的两条平行的弦,轴
上的两条平行的弦,轴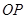 与平面
与平面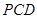 所成的角为
所成的角为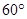 ,
,
(Ⅰ)证明:平面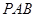 与平面
与平面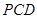 的交线平行于底面;
的交线平行于底面;
(Ⅱ)求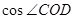 .
.
(Ⅰ)见解析
(Ⅱ)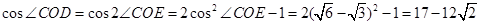
【解析】由公理可知,两面相交必交于一条直线,设面 与面
与面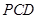 的交线为
的交线为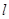
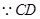 ∥
∥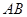
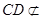 面
面 ,而
,而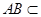 面
面
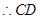 ∥面
∥面
而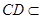 面
面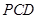
面
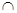 面
面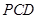 =
=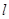
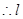 ∥
∥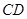
而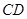
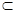 底面
底面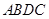
所以,平面 与平面
与平面 的交线平行于底面
的交线平行于底面
(2)
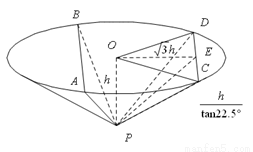
取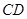 的中点
的中点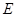 ,连接
,连接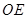 ,
,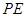 ,则
,则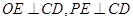
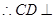 面
面 ,
,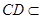 底面
底面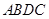
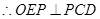
所以直线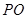 在面
在面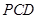 上的射影为
上的射影为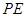
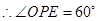
设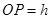 ,则
,则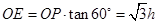
由题意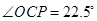
则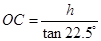
而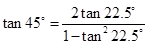 ,
,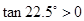 ,解得
,解得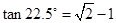
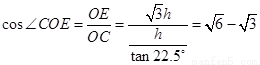
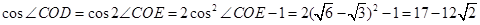
本题一反常态,考查旋转体的特征,考生一时有点迷惑,但只要静下心来,这道题其实不难.第(1)题,考生要知道两面相交必交于一条直线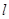 ,接着只需根据线线平行证明线面平行,而线线平行又要通过线面平行来证明,理顺这个关系,这道题就可以准确的证出了,通过这道题提醒考生课本上一些证明的定理和性质要熟练掌握.第(2)题,考生先要找出母线与底面所成的角是
,接着只需根据线线平行证明线面平行,而线线平行又要通过线面平行来证明,理顺这个关系,这道题就可以准确的证出了,通过这道题提醒考生课本上一些证明的定理和性质要熟练掌握.第(2)题,考生先要找出母线与底面所成的角是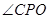 ,设
,设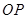 的长度表示出
的长度表示出 ,接着要能找出
,接着要能找出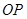 与平面
与平面 所成的角,利用这个角度求出
所成的角,利用这个角度求出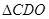 高的长度,再利用三角函数二倍角公式,三角形中的位置关系最终求出
高的长度,再利用三角函数二倍角公式,三角形中的位置关系最终求出 的值.
的值.
【考点定位】考查空间直线与直线,直线与平面,平面与平面的位置关系,线面垂直,面面垂直,直线与面所成的角等知识.


科目:高中数学 来源: 题型:
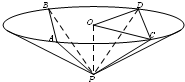 (2013•安徽)如图,圆锥顶点为P,底面圆心为O,其母线与底面所成的角为22.5°,AB和CD是底面圆O上的两条平行的弦,轴OP与平面PCD所成的角为60°,
(2013•安徽)如图,圆锥顶点为P,底面圆心为O,其母线与底面所成的角为22.5°,AB和CD是底面圆O上的两条平行的弦,轴OP与平面PCD所成的角为60°,查看答案和解析>>
科目:高中数学 来源:2013年普通高等学校招生全国统一考试安徽卷理数 题型:044
如图,圆锥顶点为p.底面圆心为o,其母线与底面所成的角为22.5°.AB和CD是底面圆O上的两条平行的弦,轴OP与平面PCD所成的角为60°

(Ⅰ)证明:平面PAB与平面PCD的交线平行于底面;
(Ⅱ)求cos∠COD.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,圆锥顶点为![]() 。底面圆心为
。底面圆心为![]() ,其母线与底面所成的角为22.5°。
,其母线与底面所成的角为22.5°。![]() 和
和![]() 是底面圆
是底面圆![]() 上的两条平行的弦,轴
上的两条平行的弦,轴![]() 与平面
与平面![]() 所成的角为60°,
所成的角为60°,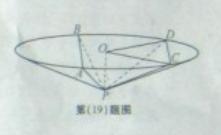
(Ⅰ)证明:平面![]() 与平面
与平面![]() 的交线平行于底面;
的交线平行于底面;
(Ⅱ)求![]() 。
。
查看答案和解析>>
科目:高中数学 来源:2013年安徽省高考数学试卷(理科)(解析版) 题型:解答题
 如图,圆锥顶点为P,底面圆心为O,其母线与底面所成的角为22.5°,AB和CD是底面圆O上的两条平行的弦,轴OP与平面PCD所成的角为60°,
如图,圆锥顶点为P,底面圆心为O,其母线与底面所成的角为22.5°,AB和CD是底面圆O上的两条平行的弦,轴OP与平面PCD所成的角为60°,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com