


图1-1-17 图1-1-18
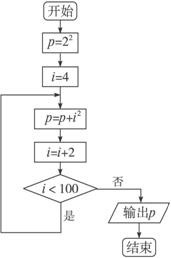

图1-1-19 图1-1-20
(1)其中正确的流程图有哪几个?错误的流程图有哪几个?错误的指出错在哪里.
(2)在错误的程序流程图中,所说的算法能运行到底吗?若能,输出的结果是什么?
(3)根据上面的回答总结出应用循环结构应该注意什么问题?
思路分析:本题考查循环结构的几个方面:计数变量、累积变量、限制条件等.对于此题我们还是从三个方面入手:
①循环变量设为i,则因为底数2,4,6, …,故初始值为i=2,且增量为2,即i=i+2;
②循环体为求22+42+62+…+1002,故应设计为p=p+i2;
③循环体要运行50次,因此循环结束条件为:当i≤100时循环运行,直到i>100时退出.
解:(1)按照这个分析,算法流程图正确的只有第4个图.
(2)图1-1-17能运行到底,但是结果是p=22+42+(42+1)+(42+2)+ …+(42+84);
图1-1-18由于无法控制循环的流程,所以算法无法运行;
图1-1-19由于只循环49次,输出的结果是22+42+62+…+982,少了1002.
(3)应用循环结构解决问题时,特别应该注意两个变量:循环变量,累积变量,以及循环控制条件.
对于循环变量,应该注意怎么开始,以及如何递加或者递减;
对于循环控制条件,应该注意什么时候终止循环,循环多少次等.不要出现多一次或者少一次,或者出现死循环等;
对于判断框流出线上的“是”“否”应该标在正确的位置,仔细分析一下流程结构,不要标反了;对于流程线,要标上箭头来体现循环结构的执行次序.
误区警示 (1)图1-1-17中有三处错误.
第一处错误,i=42应该为i=4,因为程序框图中的循环变量是i,不应该为i2,如果这样循环变量每次加的不是一个定值,而原式子底数相差是2.
第二处错误,累加的应该是i2,而不是i,故应该改为p=p+i2.
第三处错误,第四个图框中的内容,应该是i=i+2,而不是i=i+1;图1-1-18中有四处错误.
第一处错误,流程图中的流程线应该有箭头,表示程序执行的顺序.
第二处错误,累加的应该是i2,而不是i,故应该改为p=p+i2.
第三处错误,判断框没加“是”“否”来控制循环流程的走向.
第四处错误,漏掉了使循环变量i变化的式子,导致i不变化,不能退出循环,应该改为i=i+2.图1-1-19中有一处错误.
判断框内的内容使得循环不正确,只能循环49次,应该改为i≤100.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
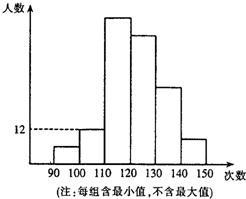 某校为了了解高一年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如下统计图,甲同学计算出前两组的频率和是0.12,乙同学计算出跳绳次数不少于100次的同学占96%,丙同学计算出从左至右第二、三、四组的频数比为4:17:15,结合统计图回答下列问题:
某校为了了解高一年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如下统计图,甲同学计算出前两组的频率和是0.12,乙同学计算出跳绳次数不少于100次的同学占96%,丙同学计算出从左至右第二、三、四组的频数比为4:17:15,结合统计图回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:
第26届世界大学生夏季运动会将于2011年8月12日至23日在深圳举行,为了搞好接待工作,组委会在某学院招募了12名男志愿者和18名女志愿者.将这30名志愿者的身高编成如下茎叶图(单位:cm):
男 女
![]() 9 15 7 7 8 9 9
9 15 7 7 8 9 9
9 8 16 1 2 4 5 8 9
8 6 5 0 17 2 3 4 5 6
7 4 2 1 18 0 1
1 19
1)根据以上茎叶图,完成以下频率分布表,并画出它的频率分布直方图。
| 分组 | 频数 | 频率 |
| [150,159) | ||
| 总计 |
2)从所列频率分布直方图估计该批志愿者的平均身高;
3)若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”。如果用分层抽样的方法从“高个子”和“非高个子”中抽取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:

图
问题1:在上图中,将QP绕Q旋转至⊙O1与⊙O2外切如图

图
问题2:继续旋转至⊙O1与⊙O2外离,如图

图
查看答案和解析>>
科目:高中数学 来源: 题型:
学校为了使运动员顺利参加运动会,招募了8名男志愿者和12名女志愿者,这20名志愿者的身高如下茎叶图(单位:cm):若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
(Ⅰ)用分层抽样的方法从“高个子”和“非高个子”中抽取5人,如果从这5人中随机选2人,那么至少有1人是“高个子”的概率是多少?
(Ⅱ)若从所有“高个子”中随机选3名志愿者,用![]() 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望.
的数学期望.
| 男 | 女 | |||||||
| 8 | 16 | 5 | 8 | 9 | ||||
| 8 | 7 | 6 | 17 | 2 | 3 | 5 | 5 | 6 |
| 7 | 4 | 2 | 18 | 0 | 1 | 2 | ||
| 1 | 19 | 0 | ||||||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com