分析:(Ⅰ)取BC中点D,连接AD,B
1D,C
1D,证明AD∥平面A
1C
1C,B
1D∥平面A
1C
1C,可得平面ADB
1∥平面A
1C
1C,从而可证AB
1∥平面A
1C
1C;
(Ⅱ)建立如图所示的坐标系,求出平面A
1C
1C的一个法向量
=(1,-1,1),
=(-2,2,0),利用向量的夹角公式,即可求得BC与平面A
1C
1C所成角的正弦值.
解答:(Ⅰ)证明:取BC中点D,连接AD,B
1D,C
1D.
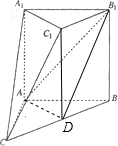
因为
B1C1BC,所以B
1C
1DB是平行四边形,
所以
C1DB1B.
又
A1AB1B,∴
A1AC1D,
所以A
1ADC
1是平行四边形
所以A
1C
1∥AD,所以AD∥平面A
1C
1C;
同理,B
1D∥平面A
1C
1C;
又因为B
1D∩AD=D,所以平面ADB
1∥平面A
1C
1C;
因为AB
1?平面ADB
1,
所以AB
1∥平面A
1C
1C; …(6分)
(Ⅱ)解:因为AB=AC,BC=
AB,所以AB
2+AC
2=BC
2,所以AB⊥AC
∵二面角A
1-AB-C是直二面角,且四边形AA
1B
1B是正方形
∴AA
1⊥平面ABC,
建立如图所示的坐标系,
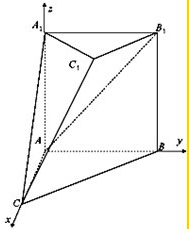
设AB=2,则A(0,0,0),B(0,2,0),A
1(0,0,2),C(2,0,0),C
1(1,1,2)
∴
=(1,1,0),
=(2,0,-2)
设平面A
1C
1C的一个法向量为
=(x,y,1)由
,可得
,∴可取
=(1,-1,1)∵
=(-2,2,0),∴cos
<,>=
=
=-
∴BC与平面A
1C
1C所成角的正弦值为
.
点评:本题考查线面平行,考查面面平行,考查线面角,考查利用空间向量解决线面角问题,确定平面的法向量是关键.

 如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=
如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=



 快捷英语周周练系列答案
快捷英语周周练系列答案 如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1
如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1 (2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,B1C1=
(2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,B1C1= (2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1=
(2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1= (2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=
(2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=