练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．函数f（x）=x-（$\frac{1}{3}$）x+a的零点在区间（1，+∞）上，则实数a的取值范围是a＜-$\frac{2}{3}$．

    分析 确定函数f（x）=x-（$\frac{1}{3}$）x+a单调递增，利用函数f（x）=x-（$\frac{1}{3}$）x+a的零点在区间（1，+∞）上，可得f（1）=$\frac{2}{3}$+a＜0，即可求出实数a的取值范围．

    解答 解：f′（x）=1-（$\frac{1}{3}$）xln$\frac{1}{3}$＞0，
    ∴函数f（x）=x-（$\frac{1}{3}$）x+a单调递增，
    ∵函数f（x）=x-（$\frac{1}{3}$）x+a的零点在区间（1，+∞）上，
    ∴f（1）=$\frac{2}{3}$+a＜0，
    ∴a＜-$\frac{2}{3}$．
    故答案为：a＜-$\frac{2}{3}$．

    点评 正确把问题等价转化、熟练掌握利用导数研究函数的单调性是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    3．若函数$f（x）=\frac{x^2}{（2x+1）（x+a）}$的图象关于y轴对称，则a=$-\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

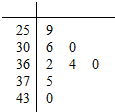    4．雾霾天气对我们身体影响巨大，据统计我市2015年12月份某8天的空气质量指数（AQI）茎叶统计图如图，则该组数据的中位数为（　　）
    A．360B．361C．362D．363

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知数列{bn}的前n项和是Sn，且bn=1-2Sn，又数列{an}、{bn}满足点{an，3${b}_{n}^{2}$}在函数y=（$\frac{1}{3}$）x的图象上．
    （1）求数列{an}，{bn}的通项公式；
    （2）若cn=an•bn+$\frac{1}{{b}_{n}}$，求数列{an}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．将函数f（x）=cos（ωx+φ）的图象向左平移$\frac{π}{2}$个单位，若所得图象与原图象重合，则ω的值不可能等于（　　）
    A．4B．6C．8D．12

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．在空间直角坐标系中，正方体ABCD-A1B1C1D1的其中四个顶点的坐标分别是D（0，0，0），A（6，0，0），C（0，6，0），D（0，0，6），若一个球与正方体ABCD-A1B1C1D1的六个面都相切，则该球的体积是36π．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知数列{an}、{bn}的每一项都是正数，a1=12，b1=8且2$\sqrt{{b}_{n}}$=$\sqrt{{b}_{n-1}}$+$\sqrt{{b}_{n+1}}$（n≥2）又bn，an，bn+1成等比数列一切n∈N*恒成立
    （1）求数列{an}、{bn}的通项公式；
    （2）设Cn=2n-1-（an-bn），若cn的前n项和为Sn，不等式Sn＞nλbn对一切n∈N*恒成立，求实数λ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．数列{an}各项均为正数，a1=$\frac{1}{2}$，且对任意的n∈N*，都有an+1=an+can2（c＞0）．
    （1）求$\frac{c}{1+c{a}_{1}}$+$\frac{c}{1+c{a}_{2}}$+$\frac{1}{{a}_{3}}$的值；
    （2）若c=$\frac{1}{2016}$，是否存在n∈N*，使得an＞1，若存在，试求出n的最小值，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知集合A={x|x2-5x+4＜0}，B={x|x≤m}，
    （1）若A⊆B，求实数m的取值范围；
    （2）若A∩B=∅，求实数m的取值范围．

    查看答案和解析>>

    同步练习册答案