
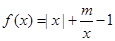
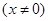 .
. 时,判断
时,判断 在
在 的单调性,并用定义证明.
的单调性,并用定义证明. ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围;
的取值范围; 零点的个数.
零点的个数.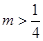 ;(3)当
;(3)当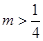 或
或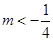 时,
时, 有1个零点.当
有1个零点.当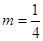 或
或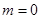 或
或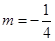 时,
时, 有2个零点;当
有2个零点;当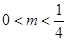 或
或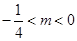 时,
时, 有3个零点.
有3个零点. ,求出
,求出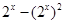 的最大值,则m的范围就是m大于
的最大值,则m的范围就是m大于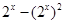 的最大值;(3)将函数零点个数转化为方程
的最大值;(3)将函数零点个数转化为方程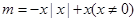 解的个数,再转化为函数
解的个数,再转化为函数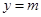 与
与 交点个数,运用数形结合思想求解.
交点个数,运用数形结合思想求解. ,且
,且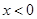 时,
时,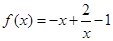 是单调递减的. 1分
是单调递减的. 1分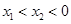 ,则
,则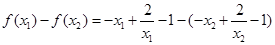

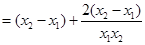
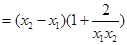 3分
3分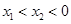 ,所以
,所以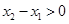 ,
,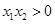 ,
,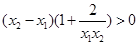
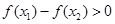 ,即
,即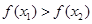 ,
, 时,
时,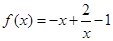 在
在 上单调递减的. 4分
上单调递减的. 4分 得
得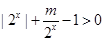 ,
,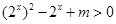 ,即
,即
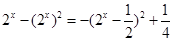 ,
,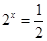 即
即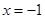 时
时 ,
,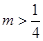 . 9分
. 9分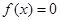 可得
可得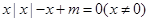 ,变为
,变为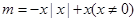
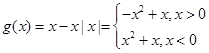
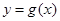 的图像及直线
的图像及直线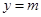 ,由图像可得:
,由图像可得: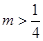 或
或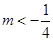 时,
时, 有1个零点.
有1个零点.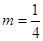 或
或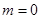 或
或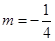 时,
时, 有2个零点;
有2个零点;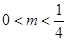 或
或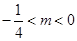 时,
时, 有3个零点. 14分
有3个零点. 14分

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源:不详 题型:解答题
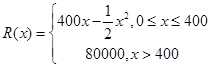 ,其中
,其中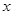 是仪器的月产量.
是仪器的月产量.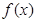 表示为月产量
表示为月产量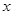 的函数;
的函数;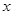 为何值时,公司所获利润最大?最大利润为多少元?
为何值时,公司所获利润最大?最大利润为多少元?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

 ,g(x)=x2,写出函数h(x)的解析式;
,g(x)=x2,写出函数h(x)的解析式;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com