
如图,在长方体 中,
中, 点
点 在棱
在棱 上.
上.

(1)求异面直线 与
与 所成的角;
所成的角;
(2)若二面角 的大小为
的大小为 ,求点
,求点 到平面
到平面 的距离.
的距离.
(1) ;(2)
;(2) .
.
【解析】
试题分析:根据几何体的特征,可有两种思路,即“几何法”和“向量法”.
思路一:(1)连结 .由
.由 是正方形知
是正方形知 .
.
根据三垂线定理得 ,即得异面直线
,即得异面直线 与
与 所成的角为
所成的角为 .
.
(2)作 ,垂足为
,垂足为 ,连结
,连结 ,得
,得 .
. 为二面角
为二面角 的平面角,
的平面角, .于是
.于是 ,根据
,根据 ,得
,得 ,又
,又 ,得到
,得到 .
.
设点 到平面
到平面 的距离为
的距离为 ,于求得
,于求得 .
.
思路二:分别以 为
为 轴,
轴, 轴,
轴, 轴,建立空间直角坐标系.
轴,建立空间直角坐标系.
(1)由 ,得
,得 ,
,
设 ,又
,又 ,则
,则 .
.
计算 得
得 即得解.
即得解.
(2) 为面
为面 的法向量,设
的法向量,设 为面
为面 的法向量,
的法向量,
由
 ,
,
得到 .①
.①
由 ,得
,得 ,根据
,根据 ,即
,即 ,
,
得到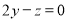 ②
②
由①、②,可取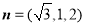 ,
,
点 到平面
到平面 的距离
的距离 .
.
试题解析:解法一:(1)连结 .由
.由 是正方形知
是正方形知 .
.
∵ 平面
平面 ,
,
∴ 是
是 在平面
在平面 内的射影.
内的射影.
根据三垂线定理得 ,
,
则异面直线 与
与 所成的角为
所成的角为 . 5分
. 5分
(2)作 ,垂足为
,垂足为 ,连结
,连结 ,则
,则 .
.
所以 为二面角
为二面角 的平面角,
的平面角, .于是
.于是 ,
,
易得 ,所以
,所以 ,又
,又 ,所以
,所以 .
.
设点 到平面
到平面 的距离为
的距离为 ,则由于
,则由于 即
即 ,
,
因此有 ,即
,即 ,∴
,∴ . .. 12分
. .. 12分
解法二:如图,分别以 为
为 轴,
轴, 轴,
轴, 轴,建立空间直角坐标系.
轴,建立空间直角坐标系.
(1)由 ,得
,得 ,
,
设 ,又
,又 ,则
,则 .
.
∵ ∴
∴ ,则异面直线
,则异面直线 与
与 所成的角为
所成的角为 . 5分
. 5分
(2) 为面
为面 的法向量,设
的法向量,设 为面
为面 的法向量,则
的法向量,则

 ,
,
∴ .①
.①
由 ,得
,得 ,则
,则 ,即
,即 ,∴
,∴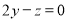 ②
②
由①、②,可取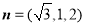 ,又
,又 ,
,
所以点 到平面
到平面 的距离
的距离 . 12分
. 12分
考点:异面直线所成的角,点到平面的距离.


科目:高中数学 来源:2013-2014学年甘肃省武威市高三数学专题训练选择填空限时练六(解析版) 题型:选择题
下图为一个算法的程序框图,则其输出的结果是( )

A.0 B.2012 C.2011 D.1
查看答案和解析>>
科目:高中数学 来源:2013-2014学年甘肃省武威市高三数学专题训练选择填空限时练一(解析版) 题型:选择题
若a,b∈(0,+∞),且a,b的等差中项为 ,α=a+
,α=a+ ,β=b+
,β=b+ ,则α+β的最小值为
,则α+β的最小值为
( )
A.3 B.4 C.5 D.6
查看答案和解析>>
科目:高中数学 来源:2013-2014学年甘肃省武威市高三数学专题训练选择填空限时练一(解析版) 题型:选择题
已知U={y|y=log2x,x>1},P= ,则∁UP=( )
,则∁UP=( )
A. B.
B.
C.(0,+∞) D.(-∞,0]∪
查看答案和解析>>
科目:高中数学 来源:2013-2014学年甘肃省张掖市高三第三次诊断考试理科数学试卷(解析版) 题型:填空题
下列结论中正确命题的序号是(写出所有正确命题的序号).
①积分 的值为2;②若
的值为2;②若 ,则
,则 与
与 的夹角为钝角;③若
的夹角为钝角;③若 ,则不等式
,则不等式 成立的概率是
成立的概率是 ;④函数
;④函数 的最小值为2.
的最小值为2.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年甘肃省张掖市高三第三次诊断考试理科数学试卷(解析版) 题型:选择题
已知 为执行如图所示的程序框图输出的结果,则二项式
为执行如图所示的程序框图输出的结果,则二项式 的展开式中含
的展开式中含 项的系数是( ).
项的系数是( ).

A.192 B.32 C.96 D.-192
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南省高三十三校第二次联考文科数学试卷(解析版) 题型:选择题
已知 都是定义在
都是定义在 上的函数,
上的函数, ,
, ,且
,且 ,
, ,
, ,对于数列
,对于数列 ,任取正整数
,任取正整数 ,则前k项和大于
,则前k项和大于 的概率是( )
的概率是( )
A. B.
B. C.
C. D.
D.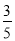
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com