解:(1)求导函数,可得
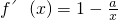
(x>0)
若a≤0,则f′(x)>0,函数在(0,+∞)上单调增,∴函数的单调增区间为(0,+∞);
若a>0,则f′(x)>0时,x>a,f′(x)<0时,x<a,∵x>0,∴0<x<a
∴函数的单调增区间为(a,+∞).单调减区间为(0,a);
(2)∵y=f(x)在x=1处取得极值,∴f′(1)=1-a=0,解得a=1
∴f(x)=x-lnx
∴f(x)+2x=x
2+b,即x-lnx+2x=x
2+b,亦即x
2-3x+lnx+b=0
设g(x)=x
2-3x+lnx+b(x>0)
则g'(x)=2x-3+

=
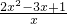
=
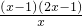
当x变化时,g'(x),g(x)的变化情况如下表
| x | (0, ) ) |  | ( ,1) ,1) | 1 | (1,2) | 2 |
| g'(x) | + | 0 | - | 0 | + | |
| G(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ | b-2+ln2 |
当x=1时,g(x)
最小值=g(1)=b-2,g(

)=b-

-ln2,g(2)=b-2+ln2
∵方程f(x)+2x=x
2+b在[

,2]上恰有两个不相等的实数根
∴g(

)≥0,g(1)<0,g(2)≥0
∴b-

-ln2≥0,b-2<0,b-2+ln2≥0
∴

+ln2≤b≤2
分析:(1)先求出函数的导函数,利用导数的正负,分类讨论,即可得到函数f(x)的单调区间;
(2)由y=f(x)在x=1处取得极值,可知f'(1)=0,从而可得函数解析式,设g(x)=x
2-3x+lnx+b(x>0),研究当x变化时,g'(x),g(x)的变化情况,确定函数的极值,利用关于x的方程f(x)+2x=x
2+b在

上恰有两个不相等的实数根,建立不等式,即可求得实数b的取值范围.
点评:本题主要考查函数的极值,考查函数的单调性,考查学生分析解决问题的能力,属于中档题.

 上恰有两个不相等的实数根,求实数b的取值范围.
上恰有两个不相等的实数根,求实数b的取值范围.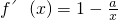 (x>0)
(x>0) =
=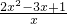 =
=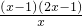
 )
)
 ,1)
,1) )=b-
)=b- -ln2,g(2)=b-2+ln2
-ln2,g(2)=b-2+ln2 ,2]上恰有两个不相等的实数根
,2]上恰有两个不相等的实数根 )≥0,g(1)<0,g(2)≥0
)≥0,g(1)<0,g(2)≥0 -ln2≥0,b-2<0,b-2+ln2≥0
-ln2≥0,b-2<0,b-2+ln2≥0 +ln2≤b≤2
+ln2≤b≤2 上恰有两个不相等的实数根,建立不等式,即可求得实数b的取值范围.
上恰有两个不相等的实数根,建立不等式,即可求得实数b的取值范围.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<