解析:(1)∵f(x)=

sinx-

cosx-

cosx+

sinx
=

(sinx-cosx)
=2sin(x-

),
∴x-

=kπ,即x=kπ+

,
∴(kπ+

,0)(k∈Z)为对称中心;
(2)∵0<α<β≤

,
∴

>β-α>0,π>β+α>0,
∵cos(β-α)=

,
∴sin(β-α)=

.
∵cos(α+β)=-

,
∴sin(α+β)=

.
∴sin2β=sin[(α+β)-(α-β)]=sin(α+β)cos(α-β)-cos(α+β)sin(α-β)=

•

-(-

)•(-

)=0,
[f(β)]
2-2=4

-2=2[1-cos(2β-

)]=-2sin2β=0,
所以,结论成立.
(3)∵f(x)=2sin(x-

),
∴f(

)+f(

)+f(

)+f(π)+f(

)+f(

)+f(

)+f(

)=0,
∴原式=251[f(

)+f(

)+f(

)+f(π)+f(

)+f(

)+f(

)+f(

)]+f(

)+f(

)+f(

)
=0+

+2
=2+

.
分析:(1)利用两角和与差的正弦与余弦及辅助角公式将f(x)转化为f(x)=2sin(x-

),利用正弦函数的性质即可求得函数图象的对称中心;
(2)利用利用两角和与差的正弦与余弦可求得sin2β=sin[(α+β)-(α-β)],再利用二倍角的余弦即可可证得结论;
(3)由f(x)=2sin(x-

),可求得f(

)+f(

)+f(

)+f(π)+f(

)+f(

)+f(

)+f(

)=0,利用函数的周期性即可求得答案.
点评:本题考查两角和与差的正弦与余弦,考查二倍角公式的应用,考查函数的周期性与函数的求值,综合题强,难度大,属于难题.

 )+cos(x-
)+cos(x- ),x∈R
),x∈R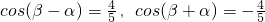 ,
, ,求证:[f(β)]2-2=0.
,求证:[f(β)]2-2=0.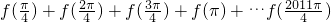 的值.
的值. sinx-
sinx- cosx-
cosx- cosx+
cosx+ sinx
sinx (sinx-cosx)
(sinx-cosx) ),
), =kπ,即x=kπ+
=kπ,即x=kπ+ ,
, ,0)(k∈Z)为对称中心;
,0)(k∈Z)为对称中心; ,
, >β-α>0,π>β+α>0,
>β-α>0,π>β+α>0, ,
, .
. ,
, .
. •
• -(-
-(- )•(-
)•(- )=0,
)=0, -2=2[1-cos(2β-
-2=2[1-cos(2β- )]=-2sin2β=0,
)]=-2sin2β=0, ),
), )+f(
)+f( )+f(
)+f( )+f(π)+f(
)+f(π)+f( )+f(
)+f( )+f(
)+f( )+f(
)+f( )=0,
)=0, )+f(
)+f( )+f(
)+f( )+f(π)+f(
)+f(π)+f( )+f(
)+f( )+f(
)+f( )+f(
)+f( )]+f(
)]+f( )+f(
)+f( )+f(
)+f( )
) +2
+2 .
. ),利用正弦函数的性质即可求得函数图象的对称中心;
),利用正弦函数的性质即可求得函数图象的对称中心; ),可求得f(
),可求得f( )+f(
)+f( )+f(
)+f( )+f(π)+f(
)+f(π)+f( )+f(
)+f( )+f(
)+f( )+f(
)+f( )=0,利用函数的周期性即可求得答案.
)=0,利用函数的周期性即可求得答案.

 启东小题作业本系列答案
启东小题作业本系列答案