
分析 先求函数的定义域,根据复合函数的单调性“同增异减”求解.
解答 解:由题意:函数f(x)=$\sqrt{{x}^{2}-2}$的定义域为{x|$x≥\sqrt{2}$或x$≤-\sqrt{2}$},
令x2-2=t,则函数f(x)=$\sqrt{{x}^{2}-2}$转化为g(t)=${t}^{\frac{1}{2}}$,(t≥0)在其定义域内为增函数.
函数t=x2-2根据二次函数的图象及性质可知:
当x在$[\sqrt{2}$,+∞)时,函数t为单调增函数,当x在$(-∞,-\sqrt{2}]$时,函数t为单调减函数,
根据复合函数的单调性“同增异减”,
∴函数f(x)=$\sqrt{{x}^{2}-2}$的单调增区间是$[\sqrt{2}$,+∞).
故答案为:$[\sqrt{2}$,+∞).
点评 本题考查了复合函数的单调性问题,要抓住定义域的范围和复合函数的单调性“同增异减”来求解.属于基础题.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | 2016+ln8 | B. | 4032+ln4 | C. | 2016+21n2 | D. | 4032+ln2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
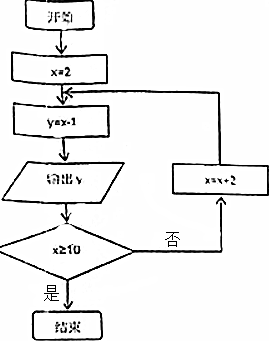 在如图所示的程序框图中,记所有的x的值组成的集合为A,由输出的数据y组成的集合为B.
在如图所示的程序框图中,记所有的x的值组成的集合为A,由输出的数据y组成的集合为B.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -2 | C. | 2 | D. | -$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com