
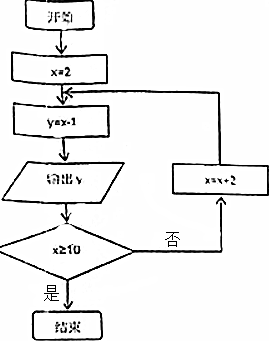
 在如图所示的程序框图中,记所有的x的值组成的集合为A,由输出的数据y组成的集合为B.
在如图所示的程序框图中,记所有的x的值组成的集合为A,由输出的数据y组成的集合为B.分析 (1)根据流程图进行逐一进行运行,求出集合A和集合B即可;
(2)先求出基本事件的总数,然后讨论满足“a>b”时包含基本事件,最后根据古典概型公式求出该概率即可.
解答 解:(1)由框图可知A={2,6,8,10},B={1,5,7,9}.
(2)其中基本事件的总数为4×4=16,
设两数中满足“a>b”为事件E,当a=2时,b=1;
当a=6时,b=1,5;
当a=8时,b=1,5,7;
当a=10时,b=1,5,7,9;
事件E包含基本事件为11,
则P(E)=$\frac{11}{16}$.
点评 本题主要考查了直到型循环结构,以及与集合和古典概型相结合等问题,算法与其他知识结合在近两年的新课标地区高考都考查到了,这启示我们要给予高度重视,属于基础题.


 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有最大值$\sqrt{5}$+1和最小值4 | B. | 有最大值5和最小值4 | ||
| C. | 有最大值5和最小值$\sqrt{5}$-1 | D. | 无最大值,最小值4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-4,0) | B. | [-4,0) | C. | (-∞,-4) | D. | (0,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com